Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 46
Duas cordas em um plano vertical exercem as mesmas forças de módulo sobre um peso suspenso, mas a tração entre elas possui um ângulo de . Qual é a força de tração que cada uma exerce, se a tração resultante é de diretamente para cima?
Passo 1
Oi, galerinha! Tudo bom?
Primeiro vamos visualizar o desenho e entender as informações fornecidas pelo problema!
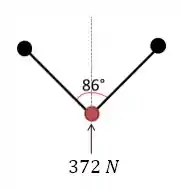
As duas cordas são idênticas e com posições simétricas, assim, as duas exercem a mesma tração na direção da tração resultante, , que é diretamente para cima.
Logo, em cada corda teremos:
Mas ele pede a força de tração que cada uma exerce, então vamos ter que considerar o ângulo para calcular.
Bora lá!
Passo 2
Temos o ângulo entre a e igual a metade de . Assim, o ângulo de cada uma com o será de (repara que a figura é simétrica e o ângulo é cortado no meio certinho).
Usando as definições das funções trigonométricas teremos:
Isolando :
O que achou? Responde Aí! 😬
