Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 45
Use componentes de vetores para determinar o módulo e a direção do vetor necessários para equilibrar os dois vetores demonstrados na Figura 1.36. Considere o vetor ao longo do eixo e considere o eixo ortogonal a ele, no sentido da direita.
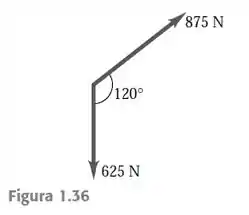
Passo 1
E aí! tudo certinho? 🤔
Nesse problema temos que criar um vetor que equilibre o sistema dado no enunciado.
O primeiro passo da questão é encontrar o vetor resultante da soma dos vetores dados.
Para estar em equilíbrio, as componentes precisam ser nulas, ou seja, basta adicionarmos um vetor contrário ao vetor resultante.
Veja só! 😁
Passo 2
Para somar dois vetores, vamos decompor cada um deles, para isso, podemos abserva-los de uma outra forma:
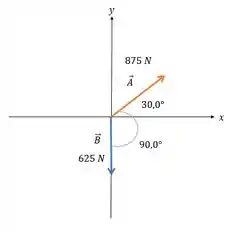
Decompondo o vetor
Decompondo o vetor
Tranquilo até aqui? 😊
Passo 3
Assim, o vetor resultante da soma dos vetores
Bacana, não é? 😉
Passo 4
Como o vetor necessário para equilibrar precisa ser oposto ao vetor resultante, temoas:
Para calcular o modulo do vetor vamos usar suas componentes:
Show? 😎
Passo 5
Para saber o sentido e a direção do vetor, vamos usar as componentes para saber o ângulo em relação ao eixo
E sabemos que:
Mas como a componente em y é positiva e a componente em x é negativa, o vetor está no segundo quadrante, logo:
E aí! o que achou? Responde Aí! 😇