Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.Problemas Adicionais - Ex. 45
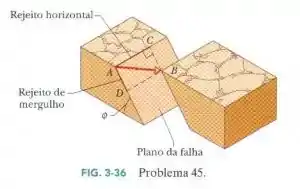
Uma falha em uma rocha é uma ruptura ao longo da qual faces opostas da rocha deslizaram uma em relação a outra. Na Fig 3-36 os pontos e coincidam antes de a rocha em primeiro plano deslizar para a direita. O deslocamento total está no plano da falha. A componente horizontal de é o rejeito horizontal . A componente de dirigida para baixo no plano da falha é o rejeito de mergulho (a) qual é o módulo do deslocamento total se o rejeito horizontal é e o rejeito de mergulho é ? (b) Se o plano da falha faz um ângulo com a horizontal, qual é a componente vertical de ?
Passo 1
Show de bolinhas galera, tudo beleza? Se liga só nesse exercício, o enunciado nos diz que a falha que ocorre em uma rocha se deve ao fato de faces opostas de uma rocha deslizarem uma em relação a outra. Nessa situação podemos medir a dimensão dessa falha através da distância final entre dois pontos que coincidiam antes da falha.
Mas calma lá galerinha, porque no primeiro momento os pontos e estavam juntinhos, mas depois da falha, os pontos se separaram formando o segmento . Isso quer dizer que se a gente calcular o tamanho do segmento , a gente vai estar encontrando a dimensão da falha que ocorreu na rocha!
Passo 2
Belezoca então pessoal, se a gente olhar somente no plano da falha, o desenho dos segmentos vai ficar desse jeito:
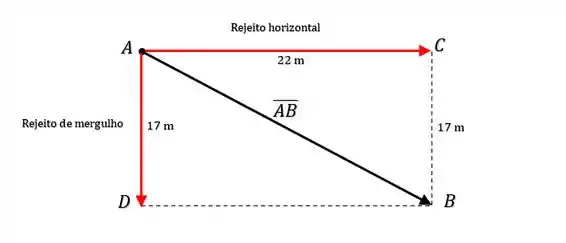
Sendo assim, na letra (a), pra gente calcular o módulo do segmento , podemos calcular a hipotenusa do triângulo , tal que:
Logo:
Passo 3
Maravilha, agora na letra (b), ele quer que a gente encontre o valor da componente vertical de , pra isso precisamos lembrar que o plano da falha faz um ângulo de com a horizontal, de forma que se a gente pegar uma vista lateral da falha, vamos ter algo desse tipo:
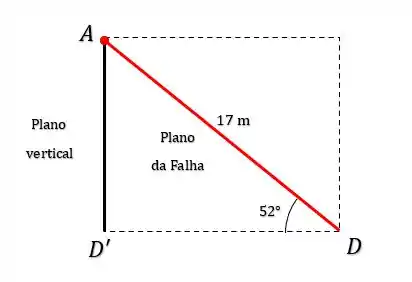
Onde é o ponto projetado no plano vertical. Desse modo, a componente vertical de vai ser dada pelo segmento . Tal que:
Logo:
Portanto:
Resposta
Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir