Uma partícula de velocidade colide elasticamente com outra idêntica em repouso. No referencial do CM, a direção de movimento é desviada de em virtude da colisão. Calcule os ângulos de deflexão, em relação à direção de movimento da partícula incidente, e as magnitudes das velocidades das duas partículas após a colisão, no referencial do laboratório.
Passo 1
Galera, a velocidade do centro de massa fica assim
Ou seja, as velocidades relativas ao centro de massa antes da colisão são
O momento linear também se conserva no referencial do CM, por isso podemos escrever
Ou seja, os vetores velocidade final formam um ângulo de entre si. Logo, se o ângulo entre e é de o ângulo entre e é de . Show!
Além disso, pela conservação de energia cnética
Tirando os termos em comum,
Agora usando a relação e substituindo os valores de velocidade inicial temos
Finalmente,
Tá, mas no que isso ajuda? Como o que queremos é o ângulo dos vetores no referencial de laboratório vamos olhar pro esquema
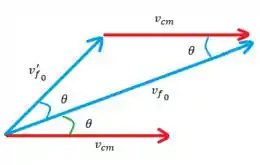
Esse triângulo é montado com base nas velocidades relativas, vejam que
Tá, o ângulo (verde) entre a linha do centro de massa e o nosso vetor velocidade final (no referencial de laboratório) é o mesmo que aquele lá de cima, por propriedade de ângulos alternos internos.
Ele também é aquele mesmo ângulo de baixo porque nosso triângulo é isósceles! Isso porque pelas continhas que fizemos ali em cima, agora sim hein!
Pronto, sabendo que o ângulo no referencial do centro de massa é , o ângulo que queremos vale . Pra a partícula 1 vale a mesma coisa, só que como vimos , ou seja, .
Passo 2
Pronto, já sabemos cada ângulo, só falta descobrir as velocidades, olhando pro triângulo de cima de novo fica assim
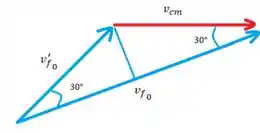
Fazendo o mesmo pra a velocidade da partícula que estava em repouso