Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 9.Problemas - Ex. 5
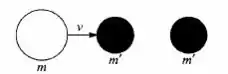
Uma partícula de massa desloca-se com velocidade em direção a duas outras idênticas, de alinhadas com ela, inicialmente separadas e em repouso (veja fig.). As colisões entre as partículas são todas elásticas. (a) Mostre que, para haverá duas colisões, e calcule as velocidades finais das três partículas. (b) Mostre que, para , haverá três colisões, e calcule as velocidades finais das três partículas. (c) Verifique que, no caso (a), o resultado para a primeira e a terceira partícula é o mesmo que se a partícula intermediária não existisse.
Passo 1
- As velocidades finais de uma colisão elástica são
- A partir de agora vamos usar para calcular a velocidade final do projétil e para calcular velocidade final do alvo, só pra gente não se confundir no meio das contas;
- Exemplo : é a velocidade final da bola 1 após a colisão (1) , é a velocidade final da bola 1 após a colisão (2) e assim por diante, fechou? Bora lá.
Como nas nossas colisões é sempre 0 já que o alvo está parado fica assim
Observações :
- Vamos observar o que acontece se
- Agora vamos usar a expressão (1) pra saber o que vai acontecer na colisão 2, que é a entre e
- Pra calcular usaremos (2) de novo, lembrando que a partícula 2 nesse caso é alvo
- Recapitulando a velocidade final da bola 1
- Recapitulando a velocidade final da bola 2
Aqui vamos ter um número negativo multiplicando o momento da partícula, ou seja
Aproveitando pra calcular a velocidade final temos
A primeira partícula que vinha em um sentido agora o inverte de modo que não vai colidir de novo com a partícula 2.
Nessa colisão e por isso
Concluímos então que
Ou seja, a bolinha intermediária fica parada no choque! Então necessariamente só há 2 colisões já que a primeira bola vai pra lá
Pra calcular a velocidade de novo bora usar (2). Saca só
Wow, a bolinha 3 fica com a velocida final igual à velocidade que a bolinha 2 pegou na colisão 1, lembrando que . Então é como se a bola do meio não existisse, por que a terceira bola pega exatamente a mesma velocidade final que pegaria se fosse só uma colisão dupla, show! Já provamos nossa letra c)
Juntando as 2 fórmulas descobrimos que
Passo 2
(Nesse caso )
Ok, nesse momento podemos garantir que a bola 1 não vai colidir de novo com a bola 2 porque a velocidade de 2 é bem maior que a de 1. ( Mas 1 continua indo para frente e futuramente quem sabe o que vai rolar? Rs )
Quando ocorrer a colisão da bola 2 com a 3 já vimos que a velocidade final de 2 vai ser 0... Opa, então com certeza a bola 1 vai atingir a 2 depois disso, show! A velocidade de 3 vai ser a mesma do problema anterior, dado por
Agora é só calcular as duas velocidades finais da terceira colisão utilizando exatamente as mesmas fórmulas de antes, moleza né?
O detalhe só é que é . Bora substituir
Última coisa ( prometo! ) : pra garantir que só hajam 3 colisões as velocidades finais da bola 1 e 2 após a terceira colisão não podem ser maiores que a velocidade final da bola 3
Vamos reescrever a velocidade final da bola 3 e comparar com essas que achamos agora
Legal, então se olharmos para as 3 fórmulas
Ae, finalmente conseguimos! Bora treinar mais?