Uma patinadora e um patinador estão se aproximando um do outro, deslizando com atrito desprezível sobre uma pista de gelo, com velocidades de mesma magnitude, igual a 0,5 m/s. Ela tem 50 Kg, carrega uma bola de 1Kg e patina numa direção 10 a leste da direção norte. Ele tem 51 Kg, dirige-se 10 a oeste da direção norte. Antes de colidirem, ela lança a bola para ele, que a apanha. Em consequência, passam a afastar-se um do outro. Ela se move agora com velocidade 0,51 m/s , numa direção a oeste da direção norte. a) Em que direção se move o patinador depois de apanhar a bola? b) Com que velocidade? c) Qual foi o momento transferido da patinadora para o patinador? d) Com que velocidade e em que direção a bola foi lançada? [Note que a deflexão das trajetórias produzida pela troca da bola é análoga ao efeito de uma força repulsiva entre os dois patinadores. Na física das partículas elementares, a interação entre duas partículas é interpretada em termos de troca de uma terceira partícula entre elas] .

1. Como há muitas informações no problema a ideia agora é esboçar a situação e organizar com eixo de coordenadas e tudo o mais pra gente se situar, vem comigo!

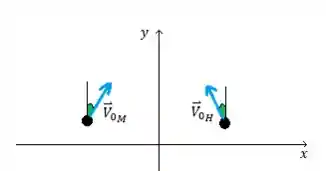
• Situação inicial



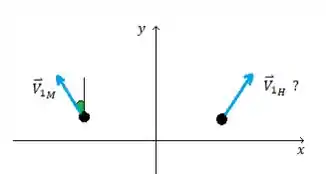
• Situação final



• No começo a mulher de massa segura a bola de massa . O momento inicial fica

Usando nosso sistema de coordenadas para decompor os vetores

Vamos agora juntar tudo o que tem na coordenada e o tudo o que tem no

• Na situação final o homem quem carrega a bola mas tem sua velocidade desconhecida

Como nenhuma força externa atua no sistema vamos escrever

Juntando nossos 2 resultados

Dividindo uma pela outra

Então ele se move

Pra saber é só substituir em uma das equações