Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 8.Problemas - Ex. 11

a) Ache as coordenadas do CM( centro de massa) da placa homogênea OABCD indicada na figura, dividindo-a em três triângulos iguais. b) Mostre que se obtém o mesmo resultado calculando o CM do sistema formado pelo quadrado OABD e pelo triângulo BCD que dele foi removido, atribuindo massa negativa ao triângulo.

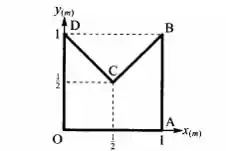
Passo 1

  1. O 3 triângulos são esses

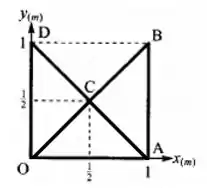
    2. Pra calcular o centro de massa total, vamos calcular os centros de massa de cada triângulo que estão em seus respectivos baricentros ( ficam a 2 3 do vértice do triângulo).

  • Triângulo OCD

    • r ⃑ 1 = 1 6   , 1 2  

    m a s s a = M

  • Triângulo OCA

    • r ⃑ 2 = 1 2 , 1 6

    m a s s a = M

  • Triângulo CAB

    • r ⃑ 3 = 1 2 + 2 3 . 1 2   , 1 2

    = 5 6 , 1 2  

    m a s s a = M

    x C M = M 6 + M 2 + 5 M 6 3 M

    = 9 M 6 3 M

    = 1 2   m e t r o

    y C M = M 2 + M 6 + M 2 3 M

    = 7 M 6 3 M

    = 7 18   m e t r o s

    Passo 2

  • Aqui é só usar o centro de massa massa do quadrado e do triângulo de cima como se sua massa fosse negativa.

  • Para o quadrado

    • r ⃑ 1 = 1 2 , 1 2

    m a s s a = 4 M

  • Para o triângulo

r ⃑ 2 = 1 2   , 1 2 + 2 3 . 1 2

= 1 2 , 5 6

m a s s a =   - M

x C M = 4 M 2 - M 2 4 M - M

= 3 M 2 3 M

= 1 2   m e t r o

y C M = 4 M 2 + - 5 M 6 3 M

= 7 M 6 3 M

= 7 18   m e t r o s

Resposta

C M ⃑ = 1 2 , 7 18

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma lata homogênea tem uma massa de 0,140k g , uma altura de 12,0c m e contém 0,354k g de refrigerante (Fig. 9-41). Pequenos furos são feitos na base e na tampa (com perda de massa desprezível) para d
Quais são (a) a coordenada x e (b) a coordenada y do centro de massa da placa homogênea da Fig. 9-38 se L = 5,0c m ?
Na molécula de amônia ( N H 3 ) da Fig. 9-40, três átomos de hidrogênio (H) formam um triângulo equilátero, com o centro do triângulo a uma distância d = 9,40 × 10 - 11m de cada átomo de hidrogênio. O
A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
(a) A que distância do centro da Terra se encontra o centro de massa do sistema Terra- Lua? (O Apêndice C fornece as massas da Terra e da Lua e a distância entre os dois astros .) (b) A que porcentage