29- Um pedaço de fio possui resistência igual a . Calcule a resistência de um resistor formada por fios iguais a esse quando eles são montados
lado a lado, formando um cabo com o mesmo comprimento do pedaço de fio considerado
conectados pelas extremidades, formando um fio com um comprimento vezes maior do que o pedaço de fio inicial.
Passo 1
No caso da letra é como se tivéssemo o seguinte esquema
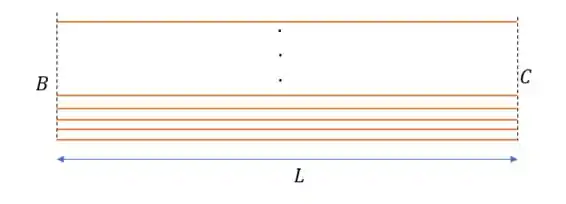
Onde o fio vai do ponto até o ponto tendo um comprimento de . E cada fio tem sua resistividade e área de seção transversal igual a .
Logo:
E quando colocamos 120 fios lado a lado da seguinte maneira nós estaremos aumentado a área da seção transversal em vezes, nos dando uma nova resistência igual a:
É dessa forma (mais ou menos) que os fios são feitos até.
Passo 2
Já na letra nós temos o seguinte esquema:

Onde agora só estamos aumentando o valor de em vezes nos dando uma fórmula tal:
Essa é uma base para o que mais tarde vai ser resistência em série e paralelo, guarde essa conhecimento para daqui a um capítulo ou dois sla hahah