Uma pedra grande é expelida verticalmente de baixo para cima por um vulcão com velocidade inicial de . Despreze a resistência do ar.

a) Qual é o tempo que a pedra leva, após o lançamento, para que sua velocidade seja dede baixo para cima?

b) Qual o tempo que a pedra leva, após o lançamento, para que sua velocidade seja de de cima para baixo?

c) Quando o deslocamento da pedra é igual a zero?

d) Quando a velocidade da pedra é igual a zero?

e) Qual o módulo e o sentido da aceleração enquanto a pedra i) Está se movendo de baixo para cima? ii) Está se movendo de cima para baixo?

iii) Está no ponto mais elevado da sua trajetória?

f) Faça gráficos , e yt para o movimento.

Agora temos que, que a velocidade, é de (aqui usamos o sinal negativo porque mudamos o sentido):

Para o deslocamento final ser zero, temos que a pedra e retorna para o mesmo ponto.

Vamos analisar os dados:

A partir desses, podemos utilizar a equação a seguir:

Isolando , temos que:

Queremos o tempo, então vamos utilizar a formula da velocidade em um intante de tempo, . E isolar o :

Mas antes, vamos analisar os dados:

A aceleração é de , para baixo, em todos os pontos do movimento.

Agora a gente vai desenhar os gráficos , e yt para o movimento. Juntando as informações que a gente tem até agora podemos fazer:

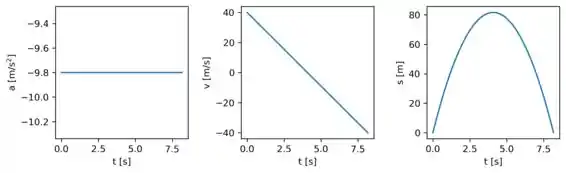
Como a aceleração é constante, nosso primeiro gráfico, , é representado por uma reta.

No gráfico temos um movimento uniformemente variado.

E no último gráfico, , temos o movimento que a pedra realiza em cada instante de tempo, .