Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.5 - Ex. 43
Um foguete de é lançado verticalmente da plataforma com uma aceleração constante no sentido de baixo para cima de e não sente nenhuma resistência significativa do ar. Ao atingir uma altura de ,seus motores falham repentinamente, de modo que a única força atuando sobre ele nesse momento é a gravidade.
a) Qual é a altura máxima que esse foguete atingirá a partir da plataforma delançamento?
b) A partir da falha no motor, quanto tempo decorrerá antes que o foguete caia sobre a plataforma de lançamento e qual será sua velocidade instantes antes da queda?
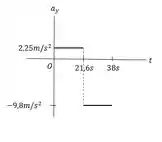
c) Faça gráficos,e ytdo movimento do foguete, do instante do lançamento até o instante da queda.
Passo 1
Opa, bora resolver esse problema! Temos um foguete saindo da plataforma com uma aceleração de até a altura de quando o motor para!
Sabendo disso a primeira coisa que a gente deve responder é a altura máxima que esse foguete atingirá a partir da plataforma delançamento!
Vamos analisar o problema, o foguete parte do repouso, com . Ele fará uma trajetória estritamente vertical e orientada para cima.
Inicialmente, precisamos saber a velocidade descrita pelo foguete no instante em que seus motores param. Como ainda não temos nenhum valor de tempo, a equação de Torricelli é suficiente. Assim:
Passo 2
- Tendo a velocidade no instante em que o motor cessa, será possível calcular a altura máxima atingida.
- O tempo total gasto pelo foguete para retornar ao solo após a falha dos motores consiste na soma do tempo de subida depois do pane mais o tempo de queda após alcançar a altura máxima.
- Primeiro, precisamos encntrar o tempo de decolagem até a falha do motor:
A altura máxima consiste dos 525m alcançados com o motor ligados mais a distância que o foguete continua a percorrer mesmo com os motores parados.
Novamente, por Torricelli:
Então temos que o foguete percorreu por com os motores ligados e aproximadamente com os motores desligados.
Passo 3
Primeiro, vamos calcular o tempo de subida após a falha:
Agora vamos calcular o tempo para sua queda:
Logo,
Além disso, podemos encontrar a velocidade no instante imediatamente anterior a queda através da relação:
Nós partiremos do momento em que o foquete atinge a sua altura máxima ,ou seja, a velocidade inicial vale e a queda se inicia:
Como já calculamos o tempo de queda, basta substituir:
Passo 4
Temos os seguintes dados:
Então vamos utilizar a equação:
Isolando:
O momento que o foguete atinge a plataforma de lançamento se da pelo tempo a partir da falha do motor mais o insntante do lançamento até a queda:
Passo 3
O gráficoé uma linha reta com inclinação positiva de durante a fase de decolagem e com negativainclinação de após falha do motor:
O sinal da aceleração determina a curvatura de .Em o foguete retornou para :
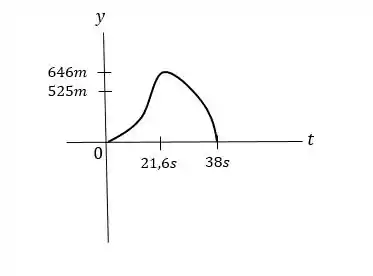
Temos uma velocidade positiva contante até o instante e depois o foguete começa a cair.
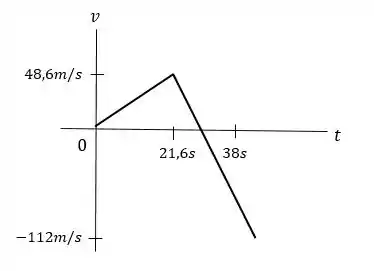
Resposta
