52. Um pêndulo de de comprimento com uma bolinha de 0,60 kg é liberado do repouso a um ângulo inicial de com a vertical. Na parte mais baixa da oscilação, a rapidez da
bolinha é de.
(a) Qunto vale ?
(b) Qual o ângulo que o pêndulo faz com a vertical quando a velocidade da bolinha é de ? Este ângulo é igual a metade de ? Explique o porquê da resposta.
Passo 1
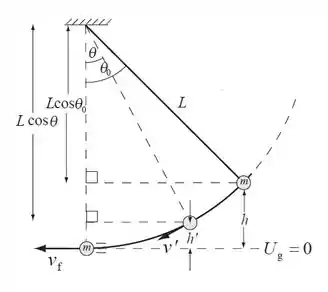
A figura mostra o pêndulo em sua posição de liberação e nas duas posições em que está em movimento, com as velocidades especificadas. Consideramos o sistema como o conjunto pêndulo e Terra e escolhemos no ponto mais baixo da oscilação.
Em seguida, o que temos que fazer, é simplesmente aplicar conservação de energia mecânica para relacionar os dois ângulos de interesse com as velocidades da bolinha em sua trajetória.
Vamos por a mão na massa!
Passo 2
a) Vamos aplicar a conservação de energia mecânica para o sistema, onde é a notação de energia cinética, é a notação de energia potencial e é o trabalho da força externa. Então, chegamos a:
Mas como , uma vez que não existem forças externas atuando temos que:
Só que e , nada mais são do que a diferença entre as energias finale e inicial e ). Com isso, obtemos que:
Agora, vamos analisar com calma o nosso problema. Considerando que o que queremos inicialmente é o valor de , vamos considerar a posiçao inicial como aquela em que oa bolinha está sendo liberada do repouso e a posição final, como aquela onde a bolinha passa pelo ponto mais baixo da trajétoria, com velocidade máxima. Bom, não é segredo pra ninguém, então, que e vão ser igual a zero. De maneira, que obtemos que:
Agora, vamos aplicar as fórmulas relativas a cada energia e conseguimos que:
Mas :
Substituindo os valores numéricos correspondentes, obtemos o valor pretendido do ângulo:
Passo 3
b) Assim como na letra a, vamos aplicar a conservação da energia mecânica para o nosso sistema. Mas desta vez, sem enrolação! Vamos direto pro que interessa
Onde e ,saõ respectivamente as energias potencial gravitacional e cinética, desta vez quando a bolinha encontra-se na altura , onde a velocidade é igual a . Logo a relação de antes ficará assim:
Ah! Esqueci de falar! é a mesma da letra a
Vamos aplicar as fórmulas relativas a cada energia, sem perder tempo:
Mas e :
Substituindo os valores numéricos correspondentes:
Logo não é igual a metade de . A explicação está no fato de que a energia potencial gravitacional é linearmente dependente do cosseno do ângulo e não do próprio ângulo.
Resposta
a)
b) , que não é metade de , porque a mudança na energia potencial gravitacional é linearmente dependente do cosseno do ângulo e não do próprio ângulo.