Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 43
43. Um bloco de massa está sobre um plano inclinado (Figura 7-44). O coeficiente de atrito estático entre o bloco e o plano é . Uma força gradualmente crescente puxa para baixo a mola (de constante de força ). Encontre a energia potencial da mola (em termos dos dados) no momento em que bloco começa a se mover.
Passo 1
Olá, querido! Cê tá bem? Então, vamos entender o que está havendo aqui.
Temos um bloco sobre um plano inclinado onde há atrito e que é puxado por uma corda ligada a uma mola. Tem bastante coisa acontecendo com esse bloco, né? Então é uma boa a gente fazer o diagrama de corpo livre desse cara:
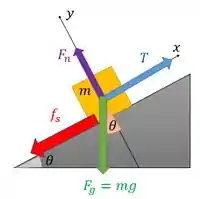
Agem no bloco quatro forças: a força normal , a força peso (, a força de atrito e a força que é a tensão na corda.
Só que a corda está ligada a uma mola que é puxada com uma força crescente. Essa força é transmitida totalmente pela mola e pela corda puxando o bloco no sentido de subir a rampa. Ou seja, a força na corda é a força aplicada na mola
Como essa força cresce gradualmente até certo ponto, em que o bloco está à beira de deslizar, a força de atrito adquire seu valor máximo, e aponta no sentido de descer a rampa.
Tá, mas o que a gente quer com tudo isso? Cara, ele pediu a energia potencial da mola quando esse bloco está à beira de deslizar. A eneria potencial de uma mola é dada por
A gente já tem a constante elástica da mola , então o que a gente precisa fazer é achar a deformação da mola . E como a gente faz isso? Bora ver!
Passo 2
Então, a gente pode achar uma expressão para aplicando a segunda lei de Newton ali no nosso diagrama. Vamos ver ele de novo aqui:
A única força fora dos eixos principais é , então vamos calcular as componentes dela:
A segunda lei de Newton tem a seguinte cara:
Como o bloco está na iminência de se movimentar na direção , vamos então usar a lei de Newton para essa situação:
Só que tem um porém. Estamos analisando o caso no qual o bloco está na iminência de movimento, justamente onde a força de atrito é máxima, . Por isso, como não há movimento ainda, a aceleração é igual a zero, o que resulta em:
Substituindo a expressão de e lembrando que :
As componentes que aparecem negativas apontam para o sentido negativo de .
Passo 3
Falta agora obter esse valor de , para a equação comecar a ficar com a cara que procuramos. Para isso, vamos realizar o somatório das forças em , no qual a aceleração também vale zero.
Agora, vamos lembrar da definição matemática da força de atrito. Ela tem essa carinha:
Mas, já obtemos anteriormente que . Assim chegamos ao valor pretendido:
Passo 4
Voltando agora, na somatório das forças na direção (equação ):
Substituindo a expressão de :
Por último, para encontrar a tão desejada deformação , basta lembrar que , na verdade, é a força na mola, aquela mesmo cuja fórmula é dada por . Só falta então fazer a última substituição na equação anterior e pronto:
Isolando quem a gente quer
Passo 5
Resta agora substituir o valor de na fórmula da energia potencial elástica:
Encontramos a nossa resposta:
Resposta