Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 35
Um pêndulo cônico é formado por uma bola de presa a um barbante de de comprimento, fazendo com que a massa se mova em um círculo horizontal com de raio. A figura mostra que, ao girar, o barbante descreve a superfície de um cone imaginário, daí o nome do dispositivo.
a. Quanto vale a tensão no barbante?
b. Qual é a velocidade angular da bola, em ?
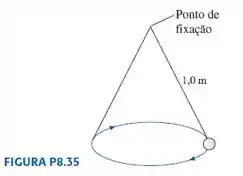
Passo 1
Olá, tudo bem?
Vamos primeiro anotar todos os dados (nas unidades do SI) que o problema nos trás:
Nesse sistema temos duas forças agindo na massa : a força gravitacional , que aponta verticalmente para baixo e a força tensora , que aponta para cima ao longo do fio.
A componente vertical da tensão vai contrabalançar a gravidade, já a componente horizontal vai ser igual à força centrípeta. Assim temos um sistema:
Para visualizar melhor, vamos fazer um esboço da situação:
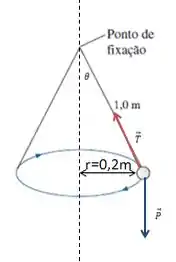
Do desenho podemos tirar o ângulo de abertura do pêndulo. Esse ângulo é formado pelo fio de sustentação de e a linha tracejada. O raio da trajetória vai ser o cateto oposto e o fio vai fazer o papel de hipotenusa. Assim com o seno conseguimos calcular o ângulo :
Daí podemos tirar a componente vertical e horizontal da tensão em função do ângulo :
E nosso sistema de equações fica:
Agora que equacionamos todo nosso problema, podemos começar a resolver o que se pede =D
Passo 2
Letra a)
Queremos saber a tensão no barbante, então da primeira equação do nosso sistema temos:
O ângulo vale , a massa é , e a gravidade vale . Então é só substituir e jogar na calculadora:
Tranquilo? Agora vamos calcular a letra (b)
Passo 3
Letra b)
Queremos a velocidade angular . E sabemos que , certo? Então da segunda equação do nosso sistema temos:
Substituindo por teremos uma expressão que relaciona a tensão (acabamos de calcular), o ângulo de abertura, o raio da trajetória e a massa. Então vamos ter uma expressão que envolve todos os valores que temos! Daí fica tranquilo pra gente resolver, saca só:
A tensão é , o vale , a massa e o raio valem e respectivamente, então basta substituir tudo e jogar na calculadora:
E por fim, devemos transformar esse valor em para . Para isso é só multiplicar o valor da velocidade que encontramos pelo fator :
Beleza?
Espero ter ajudado!
Vamos pra próxima?