Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Perguntas Objetivas - Ex. 4
Duas crianças estão em uma plataforma no topo de um escorregador curvo próximo à piscina em um quintal. No mesmo momento em que a criança menor pula diretamente para dentro da piscina, a maior se lança do topo do escorregador sem atrito.
(i) Ao chegar à água, a energia cinética da criança menor comparada à da maior é
a. Maior
b. Menor
c. Igual
(ii) Ao chegar à água, a velocidade da criança menor comparada à da maior é
a. Maior
b. Menor
c. Igual
(iii) Durante seus movimentos da plataforma para a água, a aceleração média da criança menor comparada à da maior é
a. Maior
b. Menor
c. igual.
Passo 1
(i)Amores, como a gente já discutiu em exercícios anteriores, o tempo de queda de diferentes corpos, de diferentes massas, de uma mesma altura é sempre o mesmo! Por consequência direta disso, a velocidade de queda é também a mesma!
No entanto, pensa comigo, cada corpo vai ter uma energia potencial dada pela expressão , que depende da massa de cada um.
Ao cair na piscina, a energia potencial de cada criança vai se transformar totalmente em energia cinética, dada por , que também depende da massa de cada criança, certo?
Por esse motivo, a criança menor, com menos massa, vai ter uma energia potencial menor e, consequentemente, uma energia cinética menor!
Alternativa b)
Passo 2
(ii)Como já discutido no Passo 1, sabemos que as velocidades de ambas as crianças vai ser a mesma!
Logo, alternativa c)
Passo 3
(iii)Bom, a criança maior, por descer pelo escorregador, vai ter uma aceleração um pouco diferente que a da gravidade, .
Olha esse esqueminha:
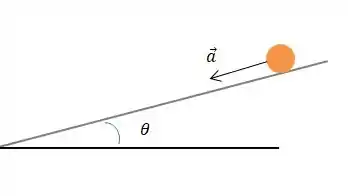
Quando um corpo cai de modo inclinado, como é o caso da criança pelo escorregador, dependendo do ângulo dessa inclinação, a aceleração de queda vai valer:
Beleza? Vale a pena guardar essa relação, muito útil sempre!
E, bom, como vai ser menor que , que seria o ângulo de inclinação com a horizontal da queda da criança menor (que se joga direto da plataforma), logo, .
Assim, o valor de , aceleração da criança maior que desce pelo escorregador, vai ser menor que o de , aceleração da criança que se joga da plataforma!
Alternativa a)
Resposta
(i) b(ii) c(iii) a