Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 62
Uma pequena bola rola ao longo de um círculo horizontal a uma altura , dentro de uma tigela esférica de raio , como mostra a FIGURA .
a. Obtenha uma expressão para a velocidade angular da bola em termos de e .
b. Qual é o mínimo valor de para que a bola consiga se mover em um círculo?
c. Quanto vale , em , se e a bola estiver na metade do caminho de subida?
Passo 1
Olá, tudo bem? Vamos começar pensando que essa bolinha deve estar localizada em algum ângulo abaixo do plano horizontal do topo dessa semiesfera. E se fizermos uma fatia nessa semiesfera na altura de , esse ângulo forma um triângulo que nos vai ser super útil. Mas pra visualizar melhor, saca só esse desenho:
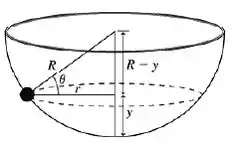
A tangente desse ângulo vai relacionar os catetos e da figura:
Passo 2
Letra a)
Bom, agora vamos ver quais forças temos aqui. A força peso aponta sempre verticalmente para baixo. Temos também a força normal, que é perpendicular à superfície de contato, então ela var ter componente vertical e horizontal. A componente vertical vai contrabalançar a força peso, certo?
E como a bolinha descreve um movimento circular, temos a força centrípeta, que é na direção radial e vai ser igual a componente horizontal da normal. Tranquilo?
Então daqui podemos tirar o seguinte sistema:
Aqui já usei a força centrípeta em função da velocidade angular, que é o que queremos, blz?
Agora vou dividir a segunda equação pela primeira (para obter a tangente!!), olha só como fica:
Agora temos uma expressão para a velocidade angular:
Passo 3
Letra b)
A velocidade angular é inversamente proporcional à distância , então quando temos o menor valor de . E usando a relação do passo anterior temos:
Passo 4
Letra c)
Se o raio é e a bolinha está na metade da subida, então , certo? Usando a expressão pra velocidade angular do passo temos:
E para transformar de para precisamos multiplicar essa velocidade pelo fator :
Beleza?
Espero ter ajudado!
Vamos pra próxima?