Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 4
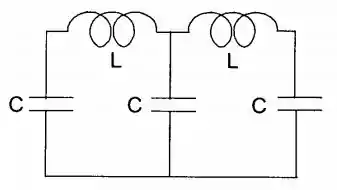
Demonstre que o circuito da figura tem duas frequências possíveis de oscilação livre, e calcule os valores dessas frequências.
Passo 1
Para resolvermos, vamos utilizar as leis de Kirchoff para circuitos em série e paralelo, somando as tensões de todo o sistema. Com isso, vamos encontrar nossa corrente que passa pelo capacitor e pelo nosso indutor, aí aplicaremos as seguintes relações
Para encontrarmos a equação que rege nosso oscilador. Após isso, tudo que teremos que fazer é manipular até encontrarmos nossas frequências de oscilação.
Passo 2
Bom, temos que o melhor método para demonstrar se o circuito tem duas frequências é calculando as mesmas. Vamos comelar então! Primeiro vamos nomear cada parte do circuito.
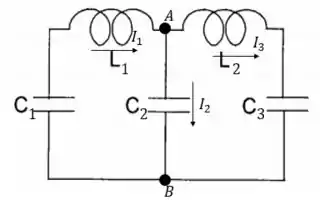
Se usarmos a segunda lei de Kirchoff nos pontos e , vamos chegar que nossas correntes respeitam a seguinte relação:
Se aplicarmos agora a primeira lei de Kirchoff, vamos encontrar três equações, dadas por:
Se manipularmos as duas primeiras, vamos chegar na nossa primeira frequência de oscilação. Teremos que:
Se derivarmos toda a expressão em relação ao tempo, teremos que
Mas como já achamos no inicio, . Assim, teremos que
Com nossa frequência .
Passo 3
Para nossa segunda frequência de oscilação, vamos manipular a ultima equação. Temos que derivando em relação ao tempo e substituindo , vamos chegar que:
Da equação do passo anterior, temos que . Assim, substituindo, vamos chegar que
Com , mostrando que temos dois valores para esse circuito.