Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 116

Um pequeno barco viaja diretamente para um porto 32 km a noroeste, quando entra numa zona de neblina. O capitão mantém a orientação noroeste, pela bússola, com uma rapidez de 10 km/h em relação à água. Depois de 3,0 h, o nevoeiro se dissipa e o capitão repara que ele está exatamente 4,0 km ao sul do porto. (a) Qual foi a velocidade média da correnteza durante essas 3,0 h? (b) O barco deveria ter viajado com qual orientação para atingir seu destino em caminho reto? (c) Qual teria sido seu tempo de viagem, se tivesse seguido esse caminho reto?

Passo 1

E aí pessoal, beleza? Vamos lá resolver esse problema. Primeiro adote um sistema de coordenadas adequado. Vamos adotar a direção norte positiva verticalmente e a direção leste positiva horizontalmente.

O enunciado nos propõe uma situação de movimento relativo. Então vamos armar nossa relação.

v → B P = v → B A + v → A P

Onde:

  • v → B P = Velocidade do barco em relação ao porto
  • v → B A = Velocidade do barco em relação a água
  • v → A P = Velocidade da água em relação ao porto

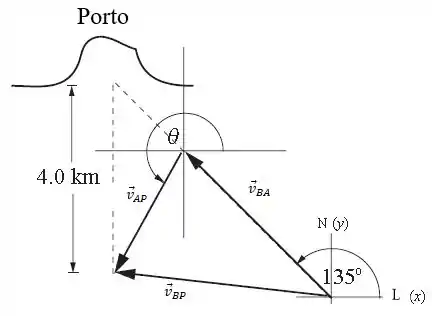
O problema nos pede a velocidade média. Ela pode ser encontrada a partir da razão entre o espaço percorrido e o tempo. Vamos descobrir qual foi o espaço percorrido:

A posição do barco após 3 horas é dada por:

r → = 32   k m ⋅ cos ⁡ 135 ° i ^ + 32   k m ⋅ sin ⁡ 135 ° - 4   k m j ^

r → = - 22,63   k m i ^ + 18,63   k m j ^

Agora que sabemos sua posição podemos relacionar com o tempo para encontrar a velocidade.

r x = 10   ⋅ cos ⁡ 135 ° + v A P ⋅ cos ⁡ θ ⋅ 3 = - 22,63

r y = 10   ⋅ sin ⁡ 135 ° + v A P ⋅ sin ⁡ θ ⋅ 3 = 18,63

Temos então que:

v A P ⋅ cos ⁡ θ = - 22,63 3 - 10 ⋅ cos ⁡ 135 ° = - 0,4723

v A P ⋅ sin ⁡ θ = 18,63 3 - 10 ⋅ sin ⁡ 135 ° = - 0,8611

Relacionando as duas equações podemos achar o valor de θ .

tan ⁡ θ = - 0,8611 - 0,4723 = 1,8232

θ = tan - 1 ⁡ 1,8232

θ = 61,26 ° ou 241,26 °

Com o valor de θ agora é possível encontrar o valor de v A P :

v A P ⋅ cos ⁡ θ = - 0,4723

v A P = - 0,4723 cos ⁡ 241,26 °

v A P = 0,982   k m / h

Passo 2

Para saber qual a orientação o barco deveria ter tomado para chegar até o porto em linha reta, levando em consideração o efeito da correnteza, devemos propor uma nova angulação e analisar. Vamos chamar essa angulação de ϕ e considerar que ela está entre o leste e a direção adequada do barco.

Temos que:

v B P x = 10 ⋅ cos ⁡ ϕ + 0,982 ⋅ cos ⁡ 241,3 °

v B P y = 10 ⋅ sin ⁡ ϕ + 0,982 ⋅ sin ⁡ 241,3 °

Como o porto está a noroeste temos que:

v B P x = - v B P y

10 ⋅ cos ⁡ ϕ - 0,472 = - 10 ⋅ sin ⁡ ϕ + 0,861

sin ⁡ ϕ + cos ⁡ ϕ = 0,1333

Com esse resultado não conseguimos fazer nada, então é necessário fazer umas manipulações trigonométricas. Atenção agora:

sin ⁡ ϕ + cos ⁡ ϕ 2 = 0,1333 2

sin 2 ⁡ ϕ + 2 ⋅ sin ⁡ ϕ ⋅ cos ⁡ ϕ + cos 2 ⁡ ϕ = 0,01777

Sabemos que sin 2 ⁡ ϕ + cos 2 ⁡ ϕ = 1 , e que 2 ⋅ sin ⁡ ϕ ⋅ cos ⁡ ϕ = s i n ⁡ ( 2 ϕ ) então:

1 + sin ⁡ 2 ϕ = 0,01777

sin ⁡ 2 ϕ = - 0,98223

2 ϕ = sin - 1 ⁡ - 0,98223

ϕ = 129,6 ° medidos a partir do leste.

Passo 3

O problema também quer saber qual o tempo de viagem, se o barco tivesse seguido essa nova direção que encontramos. Temos que:

v B P x = 10 ⋅ cos ⁡ 129,6 ° - 0,472

v B P x = - 6,846   k m / h

v B P x = v B P ⋅ cos ⁡ 135 °

v B P = - 6,846 cos ⁡ 135 °

v B P = 9,681   k m / h

Agora é só jogarmos na fórmula do tempo:

∆ t = ∆ r ∆ v = 32 9,681

∆ t = 3,3   h ou 3   h   e   18   m i n

Resposta

a ) v A P = 0,982   k m / h

b ) ϕ = 129,6 ° medidos a partir do leste.

c ) ∆ t = 3,3   h ou 3   h   e   18   m i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13 . | Um avião de suprimentos precisa soltar um pacote de alimentos para cientistas que estão trabalhando em um glaciar na Groenlândia. O avião voa a 100m de altura do glaciar com uma velocidade de 1
14 . | Um marinheiro sobe ao topo do mastro, 15 m acima do convés, para procurar por terra enquanto o navio se move constantemente a 4,0m / s em águas calmas. Infelizmente, ele deixa cair sua luneta n
12 . || Um rifle é apontado horizontalmente para um alvo a 50m de distância. A bala atinge o alvo 2,0c m abaixo do ponto central do mesmo. a. Qual foi o tempo de vôo da bala? b. Qual é a velocidade da
11 . | Uma bola arremessada horizontalmente a 25m / s percorre uma distância horizontal de 50m antes de atingir o solo. De que altura ela foi lançada?
Correndo o perigo de afundar no rio, uma criança está sendo levada pela correnteza, que flui uniformemente a 2,0m / s . A criança encontra-se a 200m da margem e 1.500m rio acima do trapiche de onde um