Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 96

Um projétil, disparado com velocidade inicial desconhecida, cai 20,0 s depois no lado de um morro, a uma distância horizontal de 3000 m do ponto inicial e 450 m acima deste ponto. (ignore a resistência do ar.) (a) Qual foi a componente vertical da velocidade inicial? (b) Qual foi a componente horizontal da velocidade inicial? (c) Qual foi a altura máxima em relação ao ponto de lançamento? (d) Ao atingir o solo, qual é sua rapidez e qual é o ângulo que o vetor velocidade forma com a vertical?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A imagem a seguir vai nos ajudar a entender melhor o enunciado:

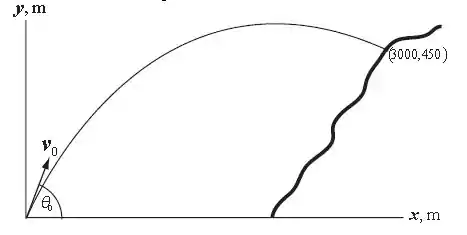
Analisando a posição verticalmente, temos:

∆ y = v 0 y t + 1 2 a y t 2

Sabemos que a aceleração é a da gravidade para baixo, logo:

∆ y = v 0 y t - 1 2 g t 2

v 0 y = ∆ y + 1 2 g t 2 t

Substituindo os valores, temos:

v 0 y = 450 + 1 2 ⋅ 9,81 ⋅ 20 2 20

v 0 y = 120,6   m / s

Passo 2

A componente horizontal da velocidade inicial é dada por:

v 0 x = v x = ∆ x ∆ t

v 0 x = 3000 20

v 0 x = 150   m / s

Passo 3

A altura máxima é dada por:

H = v 0 y t - 1 2 g t 2

Temos que:

v y = v 0 y - g t

t = v 0 y g

Aplicando na equação da altura máxima, temos:

H = v 0 y v 0 y g - 1 2 g v 0 y g 2

H = v 0 y 2 2 g

H = v 0 2 sin 2 ⁡ θ 2 g

Sabemos que:

v 0 2 = v 0 x 2 + v 0 y 2

v 0 = 150 2 + 120,6 2

v 0 = 192,5 m s

O ângulo de lançamento é dado por:

θ = cos - 1 ⁡ ∆ x v 0 ∆ t

θ = cos - 1 ⁡ 3000 192,5 ⋅ 20

θ = 38,80 °

Logo:

H = 192,5 2 sin 2 ⁡ 38,8 ° 2 ⋅ 9,81

H = 742   m

Passo 4

A velocidade final é dada por:

v = v x 2 + v y 2

v = 150 2 + - 75,6 2

v = 168   m / s

O ângulo de impacto é dado por:

θ i = tan - 1 ⁡ v y v x

θ i = tan - 1 ⁡ - 75,6 150

θ i = - 26,75 °   o u   63,3 °   c o m   a   v e r t i c a l

Resposta

a ) v 0 y = 120,6   m / s

b ) v 0 x = 150   m / s

c ) H = 742   m

d ) v = 168   m / s

θ i = - 26,75 °   o u   63,3 °   c o m   a   v e r t i c a l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pedra cai de um balão que se desloca horizontalmente. A pedra permanece no ar durante 3s e atinge o solo segundo uma direção que faz um ângulo de 30 ° com a vertical. A) Qual é a velocidade do bal
O alcance de um projétil é 4 vezes sua altura máxima, e ele permanece no ar durante 2s. a) em que ângulo ele foi lançado ? b) Qual foi a velocidade incial ? c) Qual é o alcance ?
Um canhão lança um projétil por cima de uma montanha russa de altura h, de forma a passar quase tangenciando o cume C no ponto mais alto da sua trajetória. A distância horizontal entre o canhão e o cu
Um jogador de futebol, a 20,5 m do gol adversário, levanta a bola com um chute a uma velocidade inicial de 15m/s, passando-a ao centroavante do time, que está alinhado com ele o gol a 5,5 m do gol. O
Um jogador de futebol inexperiente chuta um pênalti a 9m do gol, levantando a bola com velocidade inicial de 15 m/s. A altura da trave é de 2,4m. Calcule: a) a que distância máxima da trave, atrás do