Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 82
Um peso P é suspenso quando preso a um poste de metal vertical e uniforme, por uma corda delgada que passa por uma polia com massa e atrito desprezíveis. A corda é presa ao poste em um ponto localizado a 40,0 cm abaixo do topo e puxa no sentido horizontal em relação ao poste (Figura 11.60). O poste gira em torno de uma dobradiça na sua base, possui 1,75 m de altura e pesa 55,0 N. Um cabo delgado conecta o topo do poste a uma parede vertical. O prego que prende esse cabo à parede vai saltar, se uma força para fora maior do que 22,0 N atuar sobre ele.
a) Qual é o maior peso p que pode ser suportado dessa forma sem que o prego seja arrancado da parede?
b) Qual é o módulo da força que a dobradiça exerce sobre o poste?
Passo 1
E aí, galerinha
Nesse problema aplicaremos as condições de equilíbrio ao poste, temos que o componente horizontal da tensão no fio é 22,0 N.
O diagrama que representa o problema é
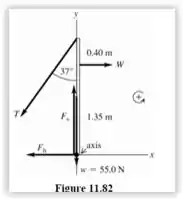
A tensão no cordão é igual ao peso W. A força vertical e a força horizontal são os componentes da força exercida pela dobradiça.
Se alguma dessas forças estiver realmente na direção oposta ao que assumimos, obteremos um valor negativo quando resolvê-lo.
Veja só!
Passo 2
Para o cálculo do maior peso, temos
Logo,
Considerando o equilíbrio
Show?
Passo 3
Para o módulo da força que a dobradiça exerce sobre o poste, fazemos a relação
Já no eixo x, temos
A força total é
E aí! o que achou? Responde Aí!
Resposta
a)
b)