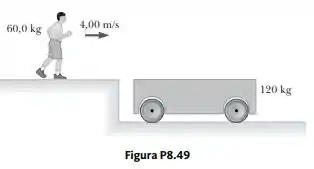
Uma pessoa de correndo a uma velocidade inicial a pula para um carrinho de inicialmente em repouso (Fig. P8.49). A pessoa desliza na superfície superior do carrinho e finalmente fica em posição de repouso. O coeficiente de atrito cinético entre a pessoa e o carrinho é. O atrito entre o carrinho e o chão pode ser ignorado. (a) Encontre a velocidade final da pessoa e do carrinho em relação ao chão. (b) Encontre a força de atrito que atua sobre a pessoa enquanto ela está deslizando pela superfície superior do carrinho. (c) Por quanto tempo a força de atrito atua sobra a pessoa? (d) Encontre a variação do momento da pessoa e do carrinho. (e) Determine o deslocamento da pessoa em relação ao chão enquanto ela desliza pelo carrinho. (f) Determine o deslocamento do carrinho em relação ao chão enquanto a pessoa desliza. (g) Encontre a variação da energia cinética da pessoa. (h) Encontre a variação da energia cinética do carrinho. (i) Explique por que as respostas de (g) e (h) são diferentes. (Que tipo de colisão é essa, e o que se leva em conta para a perda de energia mecânica?)

Letra b:

Para obter a força de atrito, primeiro consideramos a segunda lei de Newton na direção y, , que nos dá:

Letra c:

A mudança no momento da pessoa é igual ao impulso, ou:

Letra d:

A mudança no momento da pessoa é:

A mudança no momento do carrinho é:

Letra e:

Letra f:

Letra g:

Letra h:

Letra i:

A força exercida pela pessoa no carrinho deve ser igual em magnitude e oposta na direção da força exercida pelo o carrinho na pessoa. As mudanças no momento dos dois objetos devem ser iguais em magnitude e devem somar zero. Suas mudanças na energia cinética são diferentes em magnitude e não somam zero.

A distância percorrida pelo carrinho é diferente da distância percorrida pelo ponto de aplicação da força de atrito para o carrinho.

A mudança total na energia mecânica para ambos os objetos juntos, -320 J, se torna 320J de energia interna adicional nesta colisão perfeitamente inelástica.