Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 81
Um piloto de avião coloca o curso da direção de leste para oeste com uma bússola e mantém uma velocidade em relação ao ar de . Depois de voar durante , ele se encontra sobre uma cidade a a oeste e ao sul da sua posição inicial.
a) Ache a velocidade do vento (módulo, direção e sentido).
b) Se a velocidade do vento fosse igual a do norte para o sul, em que direção o piloto deveria orientar seu curso para que pudesse se dirigir de leste para oeste. Considere a mesma velocidade em relação ao ar de .
Passo 1
Oi, galerinha! Tudo bom?
Aqui temos um problema para relacionarmos velocidades relativas. Mas antes, vamos entender o que aconteceu:
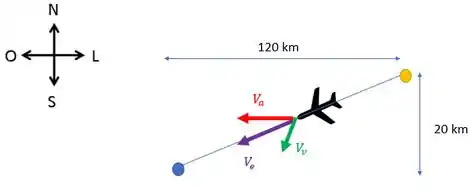
O avião saiu do ponto amarelo. Repara que piloto colocou o curso de leste a oeste com (seta vermelha). Por que ele acabou indo um pouco de norte para sul também? Cara, isso ocorre por causa da velocidade do vento, que “empurra” o avião nessa direção (seta verde).
E como a gente acha essa velocidade do vento, que o enunciado pede? A velocidade efetiva do avião em relação ao solo é a soma vetorial da velocidade do vento e a velocidade do avião em relação ao ar. Vamos achar essa velocidade efetiva primeiro pelo deslocamento do avião.
Bora lá!
Passo 2
- Os dados que o problema nos trás são:
E os deslocamentos:
Podemos calcular as componentes da velocidade em relação ao solo usando os deslocamentos e o tempo que o piloto levou para chegar a cidade
Então a velocidade efetiva é
Se a gente for escrever a velocidade do avião em relação ao ar na forma vetorial, fica assim
Agora que achamos e , podemos achar a velocidade do vento!
Tranquilo até aqui?
Passo 3
Como temos que
Substituindo:
Calculando cada componente da velocidade do vento:
Agora o módulo vai ser a raiz da soma das componentes ao quadrado:
E o ângulo :
Isso do sul para o oeste.
Show?
Passo 4
b) Cara, como ele quer que o avião ande só de leste para oeste (na horizontal no nosso desenho), precisamos que a velocidade efetiva (que dita a direção do movimento em relação ao solo) esteja na direção horizontal.
Vamos usar de novo que
Aí a gente sabe que essa velocidade do vento agora está norte para o sul. Podemos esquematizar essa soma vetorial assim:
Queremos a orientação de , a velocidade que o piloto escolhe.
Vamos chamar a velocidade do avião em relação ao ar de e a velocidade do vento de . O ângulo que queremos é .
Assim podemos relacionar o seno do ângulo com as velocidades que temos:
Isso do oeste para o norte.
Entendeu tudo? Responde Aí!
