Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 80
Um piloto voa horizontalmente a a uma altura m acima do solo inicialmente plano. No instante , o piloto começa a sobrevoar um terreno inclinado para cima de um ângulo (Figura 2-38). Se o piloto não mudar a trajetória do avião, em que instante o avião se chocará com o solo?
Passo 1
O problema nos diz que o avião está em MRU com velocidade de a uma altura de do solo e, em seguida, passa a sobrevoar um terreno com uma dada inclinação.
Já nos dados, temos que prestar atenção que a velocidade está em e a altura em . Nós precisamos unificar as unidades e, para isso, vou passar tudo para o SI. Para transformar de para precisamos dividir a velocidade por . Assim a velocidade do avião é:
Para resolver este problema, vamos usar um pouquinho de trigonometria:
Para aplicar essa relação, vamos criar um triângulo retângulo entre o avião e o plano inclinado:
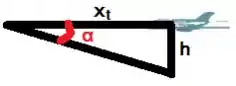
Nesse caso, usaremos o ângulo que é numericamente igual ao ângulo dado no enunciado, logo:
Passo 2
Vamos encontrar, a partir da relação trigonométrica da tangente, o tamanho do lado do triângulo retângulo:
Isolando o , temos:
Portanto, o avião terá que percorrer até colidir com o solo.
Passo 3
Com o dado da distância percorrida pelo avião na horizontal (), usaremos a função da posição de um movimento retilíneo uniforme para encontrar o instante em que, mantendo a sua trajetória, o avião colidiria com o plano inclinado ():
Considerando a origem no início do plano inclinado, então , usando a velocidade já transformada de para () e a distância () calculada no passo anterior, temos:
Isolando :
Portanto, o avião se chocará com o plano inclinado no instante , se o piloto não mudar sua trajetória.