Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 38
Uma pinha cai diretamente para baixo a partir de um pinheiro que cresceu com inclinação de . A pinha bate no solo com rapidez de 10 m/s. Qual é o componente da velocidade de impacto da pinha (a) paralelo e (b) perpendicular ao solo?
Passo 1
Eaí galerinha, vamos lá. Aqui primeito entender a situação e esboçar um diagrama de corpo livre pra ela:
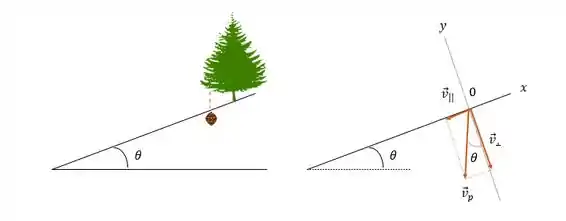
Nós conhecemos que: , e queremos encontrar e .
O sistema de coordenadas usado aqui é inclinado com o ao longo da inclinação.
Passo 2
- O componente da velocidade paralela ao é:
- O componente da velocidade perpendicular:
Esta é a velocidade da descida.
Passo 3
Esta é a velocidade em direção ao chão.
Uma velocidade de aproximadamente implica um tempo de queda de aproximadamente 1 segundo em queda livre. Observe que . Este tempo é razoável para uma queda de aproximadamente .
Resposta
Exercícios de Livros Relacionados
A posição r de uma partícula que se move no plano xy é dada por r → =2 t i →+2 sen π 4 r a d s t j → , onde r → está em metros e tem segundos. (a) Calcule os valores das componentes x e y da posição
A posição de um elétron é dada por r=3,00 t i - 4,00 t ² j+2,00 k ² ; com t em segundos e r em metros . (a) Qual é a velocidade v ( t ) do elétron na notação de vetores unitários? Quanto vale v ( t )
Um carro se move sobre um plano x y com componentes da aceleração a x = 4m / s ²ea y = - 2 m / s ² ² ². A velocidade inicial tem componentes v o x = 8m / s e v o y = 12 m / s . Na notação de vetores u
Uma partícula se move de tal forma que a posição (em metros) em função do tempo ( em segundos) é dada por r=i+4 t ² j+t k ² Escreva expressões para (a) a velocidade e (b) a aceleração em função do tem
A posição r → de uma partícula que se move em um plano x y é dada por r → = 2,0 t 3 -5,0 t i → + 6,0-7,0 t 4 j → , com r em metros et em segundos. Na notação de vetores unitários, calcule: (a) r , (b)