Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 130

A posição r de uma partícula que se move no plano xy é dada por r → =   2 t i →   +   2 sen ⁡ π 4 r a d s t j → , onde r → está em metros e tem segundos. (a) Calcule os valores das componentes x e y da posição da partícula para t   =   0   ;   1,0 ;   2,0 ;   3,0   e   4,0   s e plote a trajetória da partícula no plano x y para o intervalo O   ≤   t   ≤ 4,0 . (b) Calcule os valores das componentes da velocidade da partícula para t   =   1,0 ; 2,0   e   3,0   s . Mostre que a velocidade é tangente à trajetória da partícula e tem o mesmo sentido que o movimento da partícula em todos esses instantes traçando os vetores velocidade no gráfico da trajetória da partícula, plotado no item (a). (c) Calcule as componentes da aceleração da partícula nos instantes t   =   1,0 ;   2,0   e   3,0   s .

Passo 1

Bom pessoal , sabemos que derivando duas vezes o vetor posição r → =   2 t i →   +   2 sen ⁡ π t 4 j → , obtemos expressões para a velocidade e a aceleração:

v → = d r → d t = 2 i → + π 2 cos ⁡ π t 4 j →

a → = d v → d t = - π 2 8 sen ⁡ π t 4 j →

Passo 2

Beleza pessoal , agora só precisamos substituir os valores de t fornecidos pelo enunciado , sendo assim :

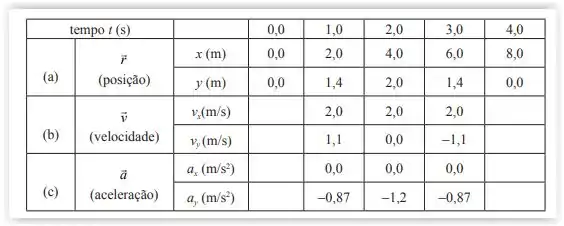
Passo 3

O gráfico , por sua vez , pode ser presentado por :

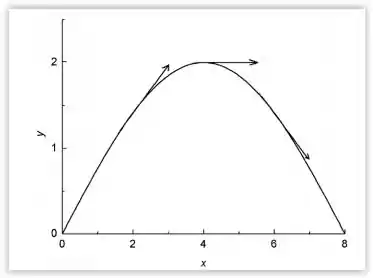
Beleza galera??? Bora resolver mais questões então!!!!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião voa 483k m para leste, da cidade A para a cidade B , em 45,0m i n , e depois 966k m para o sul, da cidade B para uma cidade C , em 1,50h . Para a viagem inteira, determine (a) o módulo e (b)
O vetor r →=5,00 t i →+ e t +f t 2 j → mostra a posição de uma partícula em função do tempo t . O vetor r → está em metros, t está em segundos e os fatores e e f são constantes. A Fig. 4-31 mostra o â
A aceleração de uma partícula que se move apenas em um plano horizontal x y é dada por a →= 3 t i →+4 t j → , onde a → está em metros por segundo ao quadrado e t em segundos. Em t= 0 , o vetor posição
Uma partícula deixa a origem com uma velocidade inicial v=( 3,00 i → )m / s e uma aceleração constante a →= ( - 1,00 i → - 0,500j → )m / s 2 . Quando a partícula atinge o máximo valor da coordenada x
A velocidade v → de uma partícula que se move no plano x y é dada por v → = 6 ,0 t - 4 ,0 t 2 i →+8 ,0j → , comv → em metros por segundo e t(0 ) em segundos . (a) Qual é a aceleração no instante t=3,0