Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 37
Jack e Jill sobem uma colina correndo a 3,0 m/s. O componente horizontal do vetor velocidade de Jill vale 2,5 m/s.
a. Qual é o ângulo de inclinação da colina?
b. Qual é o componente vertical da velocidade de Jill?
Passo 1
E aí galerinha, vamos lá. Começando aqui com um esboço para melhor visualização do problema:
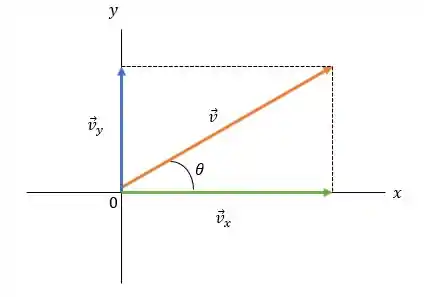
Nós conhecemos que: , e queremos encontrar e .
Passo 2
- Uma vez que:
- A componente vertical é dada por:
Nós temos que:
Passo 3
Resposta
Exercícios de Livros Relacionados
Um avião voa 483k m para leste, da cidade A para a cidade B , em 45,0m i n , e depois 966k m para o sul, da cidade B para uma cidade C , em 1,50h . Para a viagem inteira, determine (a) o módulo e (b)
O vetor r →=5,00 t i →+ e t +f t 2 j → mostra a posição de uma partícula em função do tempo t . O vetor r → está em metros, t está em segundos e os fatores e e f são constantes. A Fig. 4-31 mostra o â
Um carrinho de controle remoto está se movendo em um estacionamento vazio. A velocidade do carrinho em função do tempo é dada por [5,00 m/s (0,0180 m/s3 )t 2 ] [2,00 m/s (0,550 m/s2 )t] . (a) Determin
Se bt2 ct3 , onde b e c são constantes positivas, quando o vetor velocidade criará um ângulo de 45,0º com os eixos x e y?
A posição de uma libélula voando paralela ao solo é dada em função do tempo por [2,90 m (0,0900 m/s2 )t 2 ] (0,0150 m/s3 )t 3 . (a) Em que valor de t o vetor velocidade da libélula forma um ângulo de