Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 81

As placas de um capacitor de placas paralelas são separadas por uma distância d 0 e cada placa tem área A . Uma lâmina metálica d e área A é inserida entre as placas de maneira tal que a lâmina é paralela às placas do capacitor. (a) Mostre que a nova capacitância é dada por ε 0 A / d 0 - b , independentemente da distância entre a lâmina metálica e a placa carregada positivamente. (b) Mostre que este arranjo pode ser modelado como um capacitor que tem uma separação entre as placas em série com um capacitor cuja separação entre as placas é b , onde a + b + d = d 0 .

Passo 1

Fala galera, beleza?

A seguinte figura ilustra o enunciado.

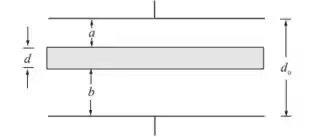
  1. Para calcular a capacitância, vamos para a definição:

    2. C = Q V

    Logo, precisamos calcular V . Para tal, sabemos que o campo elétrico entre as placas do capacitor é E = Q / ε 0 A ; já no interior do metal, o campo elétrico é nulo.

    Sendo assim, temos que

    V = E a + E b V = Q ε 0 A a + Q ε 0 A b = Q ε 0 A a + b

    Porém, temos que a + b = d 0 - d . Logo,

    V = Q ε 0 A d 0 - d

    Finalmente,

    C = Q V = ε 0 A d 0 - d

    que é o que queríamos provar.

    Passo 2

  2. Temos que

1 C = 1 C 1 + 1 C 2

onde C 1 = ε 0 A / a e C 2 = ε 0 A / b . Logo,

1 C = a ε 0 A + b ε 0 A = a + b ε 0 A

Como a + b = d 0 - d , segue que

C = ε 0 A d 0 - d

É isso, galera! :D

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitar de placas paralelas cujo dielétrico é o ar é carregado com uma diferença de potencial de 600 V. A área das placas é 40 c m 2 e a distância entre as placas é 1,0 mm. Determine(a) a capacit
Como engenheiro de segurança, o leitor precisa emitir um parecer a respeito da prática de armazenar líquidos condutores inflamáveis em recipientes feitos de material não condutor. A companhia que forn
Os dois objetos de metal da Fig. 25-24 possuem cargas de + 70 pC e -70 pC, que resultam em uma diferença de potencial de 20 V. (a) Qual é a capacitância do sistema? (b) Se as cargas mudam para + 200 p
O capacitor da Fig. 25-25 possui uma capacitância de 25 μF e está inicialmente descarregado. A bateria produz uma diferença de potencial de 120 V. Quando a chave S é fechada, qual é a carga total que
Se um capacitor de placas paralelas inicialmente descarregado, de capacitância C, é ligado a uma bateria, uma das placas, de área A , se torna negativa porque muitos elétrons migram para a superfície.