Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.3 - Ex. 3
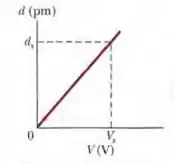
Se um capacitor de placas paralelas inicialmente descarregado, de capacitância , é ligado a uma bateria, uma das placas, de área , se torna negativa porque muitos elétrons migram para a superfície. Na Fig. 25-26, a profundidade da qual os elétrons migram para a superfície em um certo capacitor está plotada em função da tensão da bateria. A escala vertical é definida por e a escala horizontal por . Quanto vale a razão ?
Passo 1
Fala aí! Tudo certinho? 😉
Temos um capacitor de placas paralelas inicialmente descarregado, com capacitância . Esse capacitor é ligado a uma bateria. Uma das placas do capacitor, com área , se torna negativa porque muitos elétrons migram para sua superfície. A Figura 25-26 mostra a profundidade da qual os elétrons migram para a superfície em função da tensão da bateria. A escala vertical é definida por e a escala horizontal por .
Sacou? 👀
Agora, vamos calcular a razão . Para isso, precisamos entender como a profundidade varia com a tensão e relacioná-la à capacitância e à área do capacitor.
Veja só! 😁
Passo 2
Podemos calcular a carga no capacitor simplesmente multiplicando número de elétrons pela sua carga:
O número de elétrons pode ser encontrado multiplicando a densidade de elétrons, n, pela área do capacitor, A, e a profundidade da qual os elétrons migram para a superfície, assim:
Por outro caminho, podemos calcular a carga pela fórmula:
Unindo as duas equações e colocando em evidência:
Utilizando os valores dado de e :
E aí! o que achou? Responde Aí! 😉
