Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 46
PLANILHA ELETRONICA Considere que,no Problema 44,R a)Em que frequencia ?Esta frequencia particulareconhecida como frequencia 3 dB,oufpara o circuito.(b)Usando uma planilha eletronica,faca um grafico de .ondefe a trequencia.Certifique-se de que a escala estenda-se no minimo desde 10%da frequencia 3 dB ate dez vezes esta frequencia.(c)Faca um grafico de 8 versus log(parao mesmo intervalo de frequencias da Parte(b).Qualeo valor da constante de fase quando a frequencia eigual a frequencia 3 dB?
Passo 1
E ai galera!! Vamos começar aqui essa questão?? Vai ser bem rápido e eu garanto que vocês vão entender!!
Podemos usar os resultados obtidos nos Problemas 44 e 45 para encontrar e representar gráficos de versus e versus .
Letra a:
Use o resultado do Problema 44 para expressar a razão :
Quando
Eleve o quadrado de ambos os lados da equação e resolva para para obter:
Substitua os valores numéricos e avalie :
Passo 2
Letra b:
Do Problema 44 temos:
No Problema 45, foi mostrado que:
Reescreva essas expressões em termos de para obter:
Passo 3
Um programa de planilha para gerar os dados para um gráfico de versus e versus é mostrado abaixo. As fórmulas usadas para calcular as quantidades nas colunas são as seguintes:
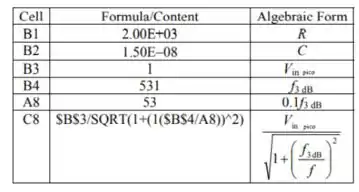
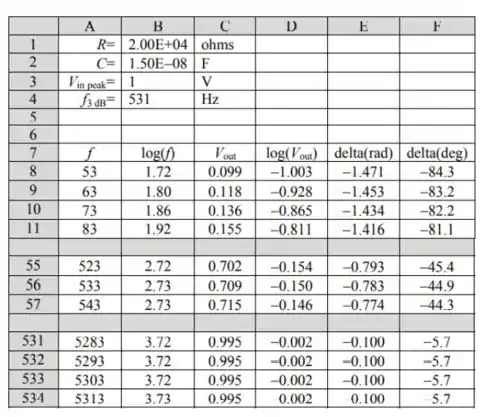
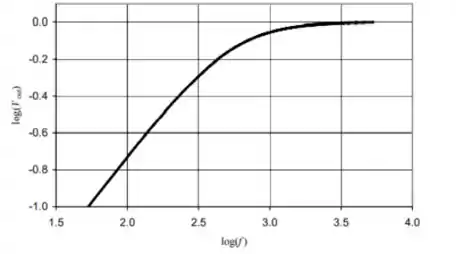
O seguinte gráfico de versus foi traçado para .
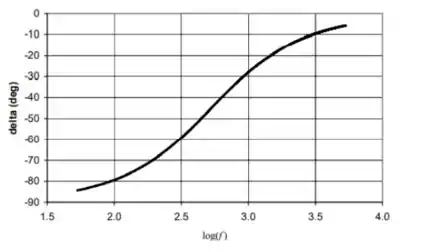
Segue um gráfico de (em graus) em função de :
Referindo-nos ao programa de planilha, vemos que quando . Este resultado está de acordo com seu valor calculado de .