Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 36.Exercícios e Problemas - Ex. 42

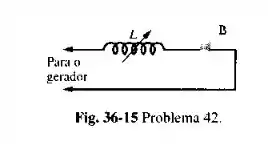
Um dimmer típico usado para regular a intensidade da luz num teatro consiste num indutor variável L (cuja indutância é ajustavel entre zero e L m á x ) ligado em série com a lâmpada B .como mostra a Fig. 36- 15.O gerador opera a 120   V r m s - 60,0   H z ; a lâmpada está assinalada por " 120 V - 1000   W " .

(a) Qual é o valor de L m á x para que a taxa de dissipação de energia na lâmpada possa ser variada por um fator igual a 5? Suponha que a resistência da lâmpada seja independente de sua temperatura.

(b) Poder-se- ia usar um resistor variável (ajustável entre zero e R m á x ) em vez de um indutor? Sendo assim,qual deveria ser o valor de R m á x ? Por que isto não é feito?

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A - A potência média dissipada na lâmpada é dada por:

P = I r m s 2 R

Onde I r m s = I 2 e I   é a amplitude da corrente, então

P = I 2 R 2   ( 1 )

Portanto, a potência máxima e mínima é dada por:

P m á x = I m á x 2 R 2   e   P m i n = I m i n 2 R 2     ( 2 )

Precisamos encontrar a indutância máxima do indutor, de modo que a potência mínima seja um quinto da potência máxima, então:

P m á x P m i n = 5

Substituindo de ( 2 ) para obter

I m á x 2 I m i n 2 = 5

As correntes são dadas por

I m á x = ε m Z m i n   e   I m i n = ε m Z m á x

Substitua na equação acima para obter:

Z m á x Z m i n 2 = 5     ( 3 )

A impedância do circuito L C é dada por

Z = R 2 + X L 2

Mas X L = L ω , então

Z = R 2 + L 2 ω 2

Passo 2

Como a resistência da lâmpada é constante, a impedância máxima ocorre quando L = L m á x e a impedância mínima ocorre quando L = 0 , daí:

Z m á x = R 2 + L m á x 2 ω 2   e   Z m i n = R     4

Substituindo em (3)

R 2 + L m á x 2 ω 2 R 2 = 5

Resolvendo para L m á x

R 2 + L m á x 2 ω 2 = 5 R 2

Isolando o L m á x

L m á x 2 = 4 R 2 ω 2 → L m á x = 2 R ω

A resistência da lâmpada pode ser determinada a partir da potência P = E 2 R → R = E 2 P , onde P é a potência da lâmpada, então (observe que ω = 2 π f ):

L m á x = ε 2 π f P

Fazendo a substituição, nós temos que

L m á x = 120 2 π ( 7,64   H z ) ( 1000   W ) = 7,64 × 10 - 2   H

Passo 3

B - Sim, podemos usar um resistor variável para fazer a mesma coisa que o indutor. Como estamos usando o resistor em série com a lâmpada, a resistência equivalente é a soma dos dois resistores, então:

R e q = R + R v

Onde R é a resistência do bulbo e R v é a resistência do resistor variável, a resistência máxima ocorre quando R v = R v , m á x e a resistência mínima ocorre quando R v = 0 , então:

R m á x = R + R v , m á x ;     R m i n = R

Substituindo em (3),

R + R v , m á x R 2 = 5

Resolvendo para R v ,   m á x

R + R v , m á x = 5 R

Isolando para R m á x

R m á x = 5 - 1 R

Como R = ε 2 P , nós temos

R m á x = 5 - 1 ε 2 P

Fazendo a substituição, nós obtemos a substituição

R v , m á x = 5 - 1 120   V 2 1000   W = 17,8   Ω

Resposta

a )   L m á x = 7,64 × 10 - 2   H

b )   R v ,   m á x = 17,8   Ω

Exercícios de Livros Relacionados

Um voltímetro de CA com uma alta impedância é ligado sucessivamente aos terminais de um indutor, aos terminais de um capacitor e aos terminais de um resistor em um circuito em série ao qual é aplicada
Num circuito RLC como o da Fig. 36-2, suponha que R = 5,00Ω ,L = 60,0m H ,f = 60,0H z e ε m = 30,0V Para que valores da capacitância a laxa média de dissipação de energia no resistor seria (a) um máxi
Na Fig. 36- 13 mostre que a taxa média com que a energia é dissipada na resistência R é máxima quando R = r , onde r é a resistência interna do gerador de c a . Até o momento, tínhamos considerado tac
A Fig.36- 14 mostra um gerador de c a ligado a uma "caixa preta" através de dois terminais. A caixa contém um circuito RLC, possivelmente até mesmo um circuito com muitas malhas, cujos elementos e lig