Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 36.Exercícios e Problemas - Ex. 40
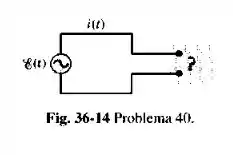
A Fig.36- 14 mostra um gerador de ligado a uma "caixa preta" através de dois terminais. A caixa contém um circuito RLC, possivelmente até mesmo um circuito com muitas malhas, cujos elementos e ligações não conhecemos. Medições externas à caixa revelam que
E
(a) Qual é o fator de potência?
(b) A corrente está avançada ou atrasada em relação à fem?
(c) O circuito na caixa é predominantemente indutivo ou capacitivo?
(d) O circuito na caixa está em ressonância?
(e) Deve haver um capacitor na caixa? Um indutor? Um resistor?
(f) Com que taxa média o gerador libera energia para a caixa?
(g) Por que não se precisa saber o valor de para responder a estas perguntas?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A fem e a corrente do gerador são dadas por:
Onde é a amplitude da fem, é a fase e é a amplitude da corrente. As medidas fora da caixa são dadas por:
Comparando essas duas equações com a equação acima, podemos ver que:
A - O fator de potência é dado por:
Substituindo os termos
B - O ângulo de fase é negativo , então:
Adicionando dos dois lados, nós temos que
Então a corrente leva a fem.
Passo 2
C - A constante de fase em termos das reatâncias e da resistência é dada por
Como , então
A diferença entre a indutância e as reatâncias capacitivas é negativa, o que significa que a reatância capacitiva é maior que a reatância da indutância, portanto, o circuito na caixa é capacitivo.
Passo 3
D - Não, o circuito não está em ressonância, pois as reatâncias não são iguais, , que é a condição da ressonância.
E – Para a fase, nós temos que
Como o valor é negativo, a reatância capacitiva e a resistência devem ter valores diferentes de zero. Portanto, a caixa deve conter um resistor e um capacitor.
F -A reatância da indutância pode ter um valor positivo menor que a reatância capacitiva ou pode ter um valor zero, então não há necessidade da caixa ter um indutor dentro dela.
G - Como dissemos na letra (e), a caixa deve conter um resistor.
Resposta
Respondido acima!!!