Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 129
A polícia do estado americano de New Hampshire usa aviões para verificar se o limite de velocidade está sendo respeitado nas rodovias. Suponha que um dos aviões possui uma velocidade de cruzeiro de no ar em repouso. Ele está voando para o norte, mantendo-se diretamente acima de uma rodovia norte-sul. Pelo rádio, um observador no solo informa ao piloto que está soprando um vento de , mas se esquece de informar a direção e o sentido do vento. O piloto observa que, apesar do vento, o avião consegue voar ao longo da rodovia em . Em outras palavras, a velocidade em relação ao solo é a mesma se não houvesse vento. (a) Qual é a direção do vento? (b) Qual é o curso do avião, ou seja, para que direção seu nariz está apontado?
Passo 1
Vamos começando dando nomes às velocidade envolvidas no problema:
Usando a fórmula de sempre para velocidade relativa, podemos escrever o seguinte:
Passo 2
Beleza, o que a gente sabe até agora? Como o avião se move diretamente acima de uma rodovia no sentido “sul para norte” sabemos que a sua velocidade em relação ao solo aponta para o norte:
E com essa velocidade ele percorre em hora nessa direção, então podemos calcular o módulo :
Além disso, como a velocidade de cruzeiro do avião no ar em repouso é , nós também sabemos o módulo da sua velocidade em relação ao vento:
Vamos representar essas informações em um desenho:
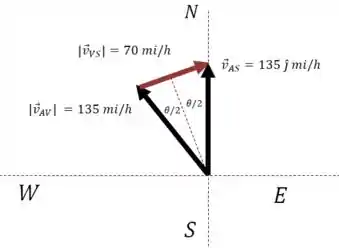
Nesse desenho, a direção do vetor e do são só chutes! Ainda vamos calcular para descobrir qual á a direção verdadeira:
Passo 3
(a) Ok, agora perceba que também é o ângulo que o vetor vermelho forma com a horizontal!
Então, pela escolha do nosso desenho o vento está soprando a ao norte do leste. Mas como também poderíamos ter desenhado o vetor no sentido oposto, também é possível que o vento esteja soprando a ao norte do oeste.
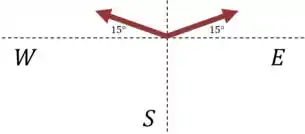
Passo 4
(b) No final das contas, o deslocamento do avião acontece na direção norte.
Mas para fazer isso, ele precisa virar o nariz com um certo ângulo em relação a essa direção, e então deixar o vento fazer a “correção” que o empurra para o norte.
Ou seja, o nariz do avião aponta na direção . Pelo nosso desenho, esse vetor forma um ângulo com a direção norte:
E isso pode ser tanto ao leste quanto ao oeste do norte, porque pode ser o ângulo no sentido horário ou anti-horário.
Quando o vento sopra ao norte do leste, o nariz do avião deve estar a oeste do norte, e vice-versa.
Resposta
(a) O vento pode estar soprando ao norte do leste, ou ao norte do oeste.
(b) Se o vento sopra ao norte do leste, o nariz do avião deve estar a oeste do norte. Se o vento sopra ao norte do oeste, o nariz do avião deve estar ao leste do norte.