Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.Problemas Adicionais - Ex. 138
138- Uma mulher é capaz de fazer um barco a remo atingir uma velocidade de 6,40 km/h em água parada.
(a) Se a mulher está atravessando um rio no qual a correnteza tem uma velocidade de 3,20 km/h, em que direção deve apontar a proa do barco para chegar em um ponto diretamente oposto ao ponto de partida?
(b) Se o rio tem 6,40 km de largura, quanto tempo a mulher levará para atravessar o rio?
(c) Suponha que, em vez de atravessar o rio, a mulher reme 3,20 km rio abaixo e depois reme de volta ao ponto de partida. Quanto tempo ela levará para completar o percurso?
(d) Quanto tempo levará para remar 3,20 km rio acima e depois remar de volta ao ponto de partida?
(e) Em que direção deve apontar a proa do barco para atravessar o rio no menor tempo possível? Qual será, nesse caso, o tempo de percurso?
Passo 1
A velocidade imposta pela mulher no barco em água corrente é a mesma que se fosse em água parada.
Para a letra a temos a seguinte representação de velocidades para que a mulher consiga chegar no ponto diagonalmente oposto.
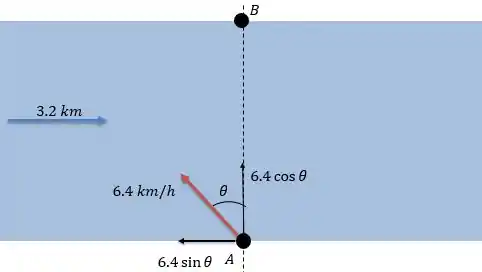
Assumindo que a correnteza está indo com sentido da esquerda para a direita, o barco deverá apontar seu bico na diagonal para a esquerda de modo que a componente horizontal de sua velocidade anule com a da correnteza, ou seja:
Isso é, o barco tem que estar apontado 30° em relação a vertical de encontro a correnteza.
Passo 2
b) Como o rio agora tem de largura temos:
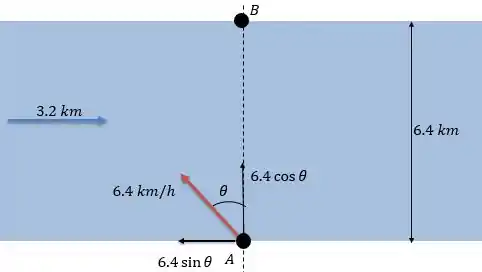
E a velocidade de atravessamento vale:
Onde , e a velocidade é uniforme perante toda a sua trajetória então.
Passo 3
c) Agora a mulher não quer mais atravessar o rio, ela percorrerá o rio perpendicularmente o rio da forma como está representado na figura abaixo:
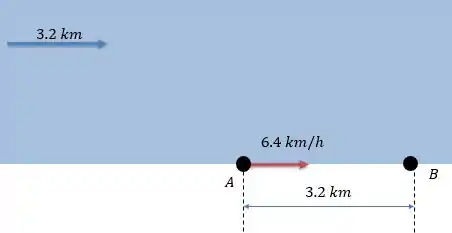
A mulher agora vai de para de modo que ela está a favor da correnteza, onde a velocidade do barco vale:
E o tempo de percurso valerá:
E depois ela volta, contra a correnteza, onde a velocidade agora vale:
Logo o tempo de percurso nesse percurso vale:
Logo o tempo total de viagem vale:
Passo 4
d) Para a letra d, a mulher faz a mesma distância só que dessa vez ela começa contra a correnteza até o ponto , depois volta para o ponto a favor da correnteza. Isso não muda o tempo que foi calculado da questão anterior:
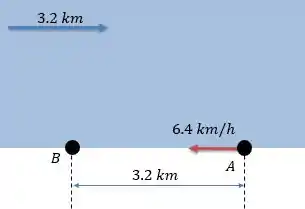
Passo 5
e) Para atravessar o rio no menor tempo possível a velocidade em direção a outra margem dve ser a maior possível e isso só acontece quando , uma vez que para qualquer diferente de zero.
O tempo de percurso será igual a:
Essa afirmação pode ser provada encontrando a fórmula do tempo, que será:
Derivando essa equação em relação a e igualando a zero temos:
Essa fração só será zero quando o numerador for zero, e ela só pode ser quando , uma vez que para a mulher não remará no rio.