Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.Problemas Adicionais - Ex. 124

124- Uma surpresa gráfica. No instante t = 0 , uma bola é lançada a partir do solo plano, com uma velocidade inicial de 16,0 m/s e um ângulo de lançamento θ 0 . Imagine um vetor posição que ligue o ponto de lançamento à bola durante toda a trajetória. Plote o módulo r do vetor posição em função do tempo para (a) θ 0 = 40,0° e (b) θ 0 = 80,0°. Para θ 0 = 40,0°, determine (c) em que instante r atinge o valor máximo, (d) qual é esse valor e a que distância (e) horizontal e (f) vertical está a bola em relação ao ponto de lançamento. Para θ 0 = 80,0°, determine (g) em que instante r atinge o valor máximo, (h) qual é esse valor e a que distância (i) horizontal e (j) vertical está a bola em relação ao ponto de lançamento.

Passo 1

Essa questão tem muitas letras então vamos de pouquinho em pouquinho resolvendo nosso problema.

Primeiramente vamos anotar os dados da questão.

A velocidade inicial da bola:

v 0 = 16   m / s

Ângulo de lançamento igual a θ 0

Letra a e b) Quer a distância r do centro da bola até a origem.

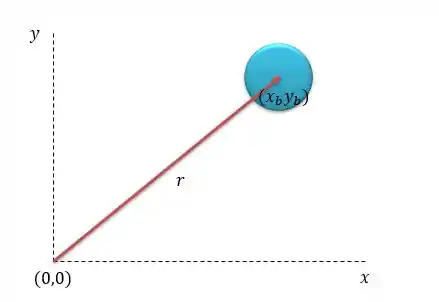
Considerando a origem no ponto igual a ( 0,0 ) temos que por Pitágoras o tamanho do vetor r .

r = y b 2 + x b 2

Onde ( y b , x b ) são as coordenadas da bola.

E as posições x e y da bola respeitam as equações da balística, que nos diz que:

x b = v x t = v o cos ⁡ θ 0 × t

E

y b = 0 + v 0 y t + 1 2 a t 2

Como a aceleração a é igual a gravidade g e é decrescente, e v 0 y = v 0 s e n   θ 0 temos:

y b = v 0 t   s e n   θ 0 - g t 2 2

Logo o vetor r terá valor igual a:

r = ( v 0 t cos ⁡ θ 0 ) 2 + v 0 t   s e n   θ 0 - g t 2 2 2  

r = v 0 2 t 2 ( cos 2 ⁡ θ 0 + s e n 2 θ 0 ) - v 0 g t 3 s e n   θ 0 + g 2 t 4 4

r = v 0 2 t 2 - v 0 g t 3   s e n   θ 0 + g 2 t 4 4

Tirando t da raiz:

r = t v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4

Passo 2

Letra a) Plotando os resultados para θ = 40 ° e v 0 = 16   m / s .

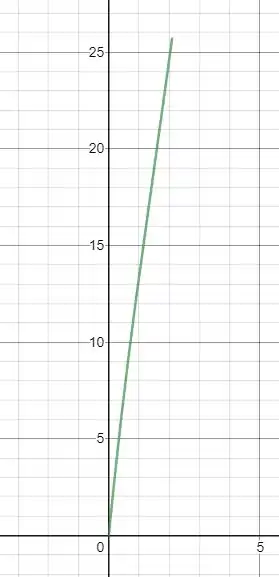
b) Agora para θ = 80 °

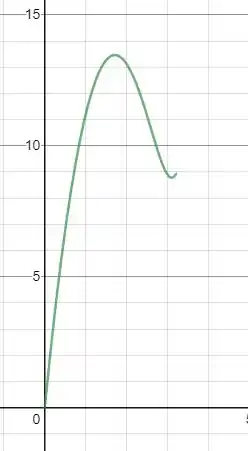
Passo 3

c) Para encontrar os pontos de máximo e mínimo precisamos saber quando que a derivada da função será zero, logo:

d r d t = 0

Fazendo a regra do produto e posteriormente a regra da cadeia encontramos:

d r d t = v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4 + t × - v 0 g   s e n   θ 0 + g 2 t 2 2 v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4

d r d t = 2 v 0 2 - v 0 g t   s e n   θ 0 + g 2 t 2 4 + - v 0 g t   s e n   θ 0 + g 2 t 2 2 2 v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4

d r d t = 2 v 0 2 - 3 v 0 g t s e n   θ 0 + g 2 t 2 2 v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4

Dividindo numerador e denominador por 2 temos:

d r d t = v 0 2 - 3 2 v 0 g t   s e n   θ 0 + 1 2 g 2 t 2 v 0 2 - v 0 g t   s e n   θ 0 + g 2 t 2 4

Substituindo v 0 = 16 e θ = 40 temos:

d r d t = 256 - 15 1.34 t + 48.12 t 2 256 - 100.9 t + 24.06 t 2

Como queremos saber somente as posições onde d r d t = 0 então somente precisamos analisar onde o numerador é zero e tentando encontrar por Bháskara as raízes do numerador nós vemos que essa equação não possui zeros. Não tendo valores de mínimos ou máximos.Assim como nos mostra o gráfico dessa função.

Logo o valor máximo de r ocorre quando a bola encosta no chão que é quando:

t t = v 0 s e n   θ g = 2 × 16 × s e n ( 40 ) 9.81 = 2.1   s

Passo 4

Para encontrar o valor de r basta substituir o valor de t na equação:

r = t v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4

Para v 0 = 16 ,   t = 2.1 ,   g = 9.81

r = 2.1 16 2 - 16 × 9.81 × 2.1 s e n 40 + 9.81 2 × 2.1 2 4 = 25.7   m

Passo 5

e) Para encontrar a distância horizontal basta fazer o que fizemos para dizer o que é x b no passo 1.

x b = v o t cos ⁡ θ = 16 × 2.1 × cos ⁡ 40 = 25.7   m

f) Por lógica, como o tempo que encontramos é o tempo total de percurso da bola logo faz sentido que y b = 0 .

25.7 2 = 25.7 2 + y 2 → y = 0

Passo 6

g) Pelo gráfico de r no passo 2 para θ 0 = 80 temos dois valores onde d r d t = 0 e por esse gráfico temos que pegar o menor.

d r d t = v 0 2 - 3 2 v 0 g t   s e n   θ 0 + 1 2 g 2 t 2 v 0 2 - v 0 g t   s e n   θ 0 + g 2 t 2 4

Para v 0 = 16 ,   g = 9.81 ,   θ 0 = 80 .

d r d t = 256 - 231.86 t + 48.11 256 - 154.58   t + 24.06 t 2

Fazendo Bhaskara nós encontramos t 1 = 1.713   s e t 2 = 3.105   s

Logo o tempo de r m a x é em t = 1.713   s

Passo 7

Agora podemos encontrar os valores da distância r , da distância horizontal e vertical assim como fizemos nos passos 4 e 5.

h)

r = t v 0 2 - v 0 g t s e n   θ 0 + g 2 t 2 4

Para t = 1.713 ,     v 0 = 16 ,     θ 0 = 80

r = 1.713 × 16 2 - 16 × 9.81 × 1.713   s e n 80 + 9.81 2 × 1.713 2 4 = 13.47   m

i)

x b = v 0 t c o s   θ = 16 × 1.713 × cos ⁡ 80 = 4.76   m

j)

r 2 = x b 2 + y b 2

y b = 13.47 2 - 4.76 2 = 12.6   m

Resposta

Letras a e b) Gráficos no passo 2.

c) t = 2.1   s

d) r = 25.7   m

e) x b = 25.7   m

f) y b = 0   m

g) 1.713   s

h) r = 13.47     m

i) x b = 4.76   m

j) 12.6   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um garoto atira uma pedra com velocidade inicial de 15 m/s, a um ângulo de 60 ° com a horizontal.A) Qual é a altura máxima atingida pela pedra?B) Qual é o módulo da sua velocidade no ponto de altura m
Qual é o módulo da velocidade do projétil cujo movimento é visto na Figura 4.12 ao colidir contra o piso?
A Figura 4.12 mostra dados sobre um projétil que atinge um ponto em um plano elevado de uma altura H em relação ao ponto de lançamento. Quanto vale H?
A Figura 4.13 mostra alguns dados da trajetória de um projétil. Calcule d em termos de v o ,φeg .
Um índio atira flechas com a velocidade de 30 m/s. Com quem inclinação θ deve ele atirar uma flecha se pretende atingir um ponto, à mesma altitude em que se encontra e à distância de 65 m, de forma qu