A posição de um corpo oscilando em uma mola é dada por , onde e são constantes. , e . (a) Plote como uma função de para . (b) Meça a inclinação do seu gráfico em para encontrar a velocidade nesse instante. (c) Calcule a velocidade média para uma série de intervalos, começando em e terminando em , , , , e . (d) Calcule para encontrar a velocidade em . (e) Compare os seus resultados nas partes (c) e (d) e explique porque seus resultados na parte (c) se aproximam dos seus resultados da parte (d).
Passo 1
(a) Nesse caso só precisamos substituir os valores e desenhar o gráfico:
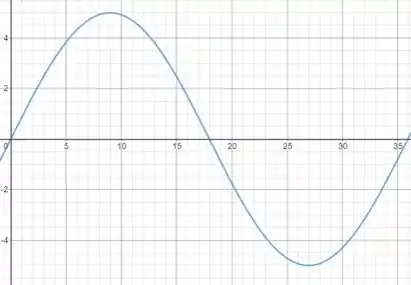
Esse é um gráfico de (em ) em função de (em ).
Passo 2
(b) Para calcular a velocidade nesse instante precisamos desenhar uma reta tangente ao gráfico no ponto , e então calcular sua inclinação.
Outra forma de fazer isso é lembrar que a função é muito próxima da função quando é próximo de zero.
E então no entorno do zero nossa função é muito próxima de , que tem inclinação . Essa é a velocidade instantânea da função nesse ponto.
Passo 3
(c) Para calcular a velocidade média em cada um dos intervalos, precisaremos usar a seguinte fórmula:
Vamos organizar os dados em uma tabela:
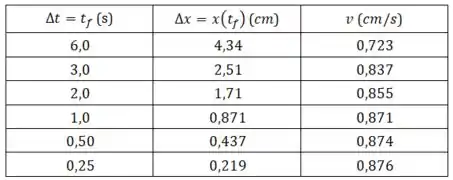
Passo 4
(d) Agora vamos calcular a velocidade em usando a definição:
Esse resultado é bem próximo do que calculamos na letra (c). Isso acontece porque, conforme os intervalos e ficam menores na nossa tabela da letra (c), mas nos aproximamos de calcular a derivada da função naquele ponto, que é justamente a definição da velocidade.
Resposta
(a) Gráfico.
(b) .
(c) Tabela.
(d) .