Um corpo, de 2,0 kg de massa, é preso à extremidade superior de uma mola cuja extremidade inferior está presa ao solo. O comprimento da mola frouxa é , e o comprimento da mola quando o corpo está em equilíbrio é . Quando o objeto está em repouso em sua posição de equilíbrio, ele recebe um forte golpe para baixo com um martelo, de modo que sua velocidade inicial é de 0,30 m / s. (a) Até que altura máxima acima do piso o objeto eventualmente se eleva? (b) Quanto tempo leva para o objeto atingir sua altura máxima pela primeira vez? (c) A mola nunca fica descomprimida? Qual velocidade inicial mínima deve ser dada ao objeto para que a mola não seja tensionada em algum momento.
Passo 1
a) Queremos a altura máxima do objeto em relação ao solo. Olha esse esqueminha:
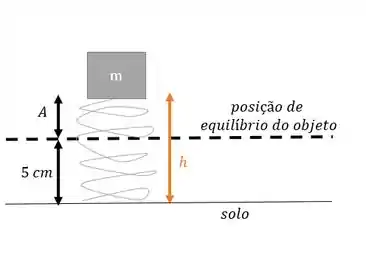
Podemos lembrar que amplitude é a distância máxima do corpo em relação a sua posição de equilíbrio (o corpo oscila em relação a posição de equilíbrio). O enunciado diz que o objeto tem seu equilíbrio numa altura de .
Então a altura máxima do objeto em relação ao solo vai ser:
Vamos achar essa amplitude.
Passo 2
O enunciado disse deu a velocidade inicial. Essa velocidade é a velocidade do objeto quando está na posição de equilíbrio. Aí precisamos lembrar que a velocidade na posição de equilíbrio é máxima.
Logo, podemos entender que essa velocidade inicial é a velocidade máxima do objeto. Então o enunciado nos dá a velocidade máxima. Assim, podemos usar a fórmulinha que relaciona a velocidade máxima do MHS com a amplitude:
Sendo a frequência angular. Escrevendo a equação de w
Isolando A da fórmula da velocidade máxima e substituindo w:
Onde é a massa do objeto e é a constante da mola.
Passo 3
E agora precisamos obter k, para isso, vamos usar a Segunda Lei de Newton para o objeto quando ele está na posição de equilíbrio, antes de receber a pancada.
Ele tem a força peso o puxando para baixo e tem a força elástica o empurrando para cima. Mas ele está parado. Então o equilíbrio de forças na vertical é
Aí muita atenção. Esse é a diferença entre a posição do objeto e a posição da mola quando ela está frouxa . Então é
Substituindo na equação da amplitude o que achamos para k
E agora substituindo na equação de h que determinamos lá em cima no passo 1
Ficamos com:
Para esse calculo ficar direitinho, precisamos escrever os centímetros em metros:
Passo 4
b) Queremos o tempo para a mola chegar na altura máxima da primeira vez.
Vamos refletir. Digamos que o movimento tem um período . Ele faz 4 caminhos dentro desse tempo.
1. O nosso objeto é batido para baixo, então ele começa saindo do equilíbrio e chega ao ponto de altura mínima.
2. Saí da altura mínima e sobe para o ponto de equilíbrio.
3. Do ponto de equilíbrio, ele sobe mais para o ponto de altura máxima
4. Da altura máxima, ele desce para voltar ao ponto de equilíbrio.
Ele leva para percorrer cada caminho desse. Assim, o tempo necessário para o objeto atingir a altura máxima pela primeira vez é três quartos do período:
Vamos então escrever a equação do período para o movimento:
Substituindo o mesmo k que achamos antes:
Colocando na expressão do tempo que escrevemos acima:
Substituindo os valores das grandezas:
Passo 5
c) Primeiro ele pergunta se a mola que a gente tá usando fica frouxa em algum momento. Ou seja, fica na altura onde ela não está tensionada de .
Cara, vimos que a altura máxima do objeto em relação ao solo é de , então esse é o ponto máximo que a mola chega, assim ela não chega em . E por isso, não fica frouxa no nosso movimento.
Passo 6
Vamos para a segunda parte da letra (c).
Nós queremos a velocidade inicial mínima para que a mola em algum momento esteja frouxa, ou seja, que esteja na altura sem tensão de . Como queremos a velocidade mínima, podemos pensar que a mola só fica frouxa quando objeto está na altura máxima dele.
Mas lembra que essa velocidade inicial é a velocidade máxima do objeto. E que a gente já tem uma expressão que relaciona altura do objeto em relação ao solo com sua velocidade máxima (velocidade inicial) que era
Então, queremos descobrir para que . Isolando :
Substituindo os dados
Obs: ficamos diferentes do gabarito nessa parte, mas estamos certinhos, beleza?
Resposta
No nosso movimento a mola não fica frouxa em nenhum momento porque