Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.6 - Ex. 18
(a) Se a posição de uma partícula é dada por ,onde está em metros e em segundos, em que instante(s) a velocidadeda partícula é zero? (b) Em que instante(s) a aceleraçãoa é zero? (c) Para que intervalo de tempo (positivo ou negativo) a aceleração é negativa? (d) Para que intervalo de tempo (positivo ou negativo) a aceleração é positiva? (e) Desenhe os gráficos de, e .
Passo 1
Belezera pessoal, temos que lembrar que a velocidade é a derivada da posição e que a aceleração é a derivada da velocidade! Então dada a equação da posição:
A velocidade será:
Enquanto a aceleração será:
Agora, basta igualar as equações a zero e encontrar os valores de que satisfazem as equações.
Logo:
E da mesma maneira:
Passo 2
Vamos fazer um estudo do sinal da aceleração?
Para resolver essa desigualdade vamos dividir dos dois lados por . lembrando que quando dividimos ou multiplicamos uma desigualdade por um número negativo ela é invertida, não se esqueça disso!
Vamos fazer o mesmo para quando a aceleração é positiva:
Então a aceleração é negativa quando e é positiva quando .
Passo 3
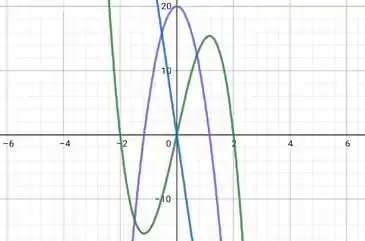
Em verde temos o gráfico , em roxo o gráfico de e em azul o gráfico de .
Resposta
a)
b)
c) negativa quando
d) positiva quando