Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.3 - Ex. 19
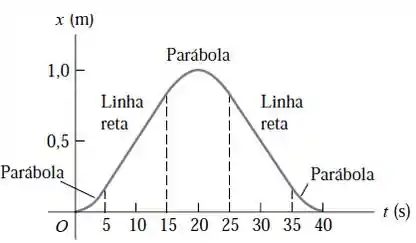
A Figura 2.35 mostra a coordenada de uma aranha que se desloca lentamente ao longo do eixo Ox.
a) Faça um gráfico de sua velocidade e aceleração em função do tempo.
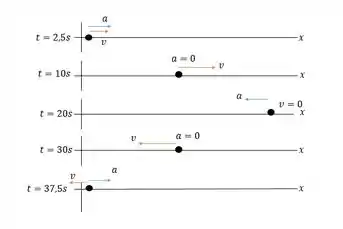
b) Faça um diagrama do movimento (como o da Figura 2.13b ou o da Figura 2.14b) mostrando a posição, a velocidade e a aceleração da aranha para cinco tempos: , , , e .
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá esse gráfico:
A primeira coisa que ele pede pra a gente é o gráfico da velocidade e aceleração da aranha em função do tempo.
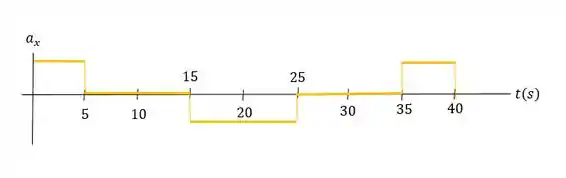
Vamos analisar o gráfico da figura 2.35:
No intervalo de tempo de a temos uma parábola, então a aceleração é uma costante, e como a curva é positiva, então a aceleração também é positiva. A velocidade é uma linha reta com inclinação positiva e a velocidade inicial é igual a zero.
No intervalo de tempo de a temos uma linha reta, ou seja, uma velocidade constante e aceleração igual a zero. Como a inclunação é positiva, a velocidade é positiva.
No intervalo de tempo de a, temos uma parábola com curvatura negativa, então temos que a aceleração é constante e negativa.
Ok! Vamos recaptular o que observamos ate agora:
A velocidade é zero a , positiva de a , e negativa de a .
Continuando:
De a temos uma linha reta, então a velocidade é constante e a aceleração é igual a zero. Mas agora observe que a inclinação dessa reta é negativa, logo a velocidade é negativa.
E no ultimo intervalo, de a temos uma parábola com curvatura positiva, então temos uma aceleração constante e positiva.
Passo 2
- Com a analise que fizemos, podemos esboçar o gráfico da aceleração e da velocidade em função do tempo:
- Ainda com a analise que fizemos do gráfico da figura 2.35:
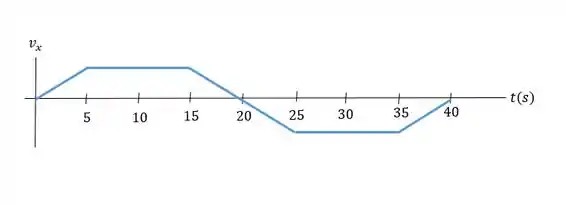
Passo 3
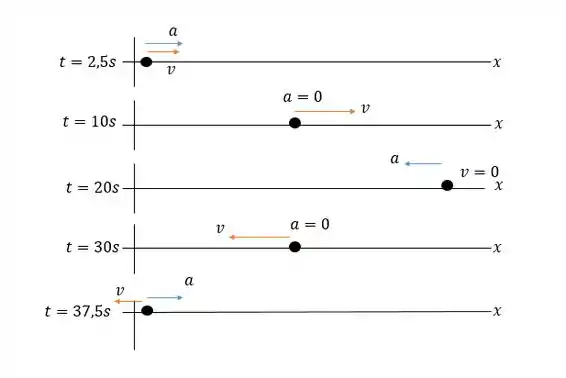
Resposta
