Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.5 - Ex. 17
A posição de uma partícula que se move ao longo do eixo x é dada por , onde está em centímetros e tem segundos. Calcule (a) a velocidade média durante o intervalo de tempo de a ; (b) a velocidade instantânea em ; (c) a velocidade instantânea em ; (d) a velocidade instantânea em ; (e) a velocidade instantânea quando a partícula está na metade da distância entre as posições em e . (f) Plote o gráfico de em função de e indique suas respostas graficamente.
Passo 1
Pessoal, para encontrar a velocidade média entre o intervalo de tempo a , precisamos descobrir o deslocamento.
Passo 2
Para resolver essa questão vamos precisar encontrar a função velocidade. Devemos lembrar que a velocidade é a derivada da função posição pelo tempo.
Substituindo e na função encontramos a velocidade em cada instante.
Passo 3
Já encontramos a posição em e em , para saber a posição entre elas basta fazer a média entre elas.
Galera, agora temos que descobrir em qual instante a partícula está em . Devemos substituir por na função posição e isolar .
Agora vamos substituir isso na função velocidade:
Resposta
a)
b)
c)
d)
e)
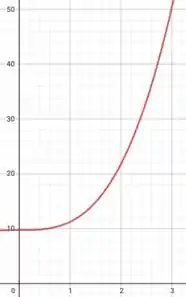
f)
