Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 17

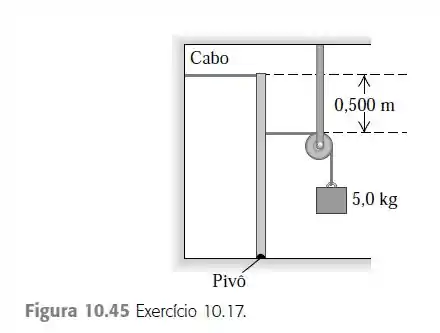
Um poste delgado e uniforme de 15,0 kg e 1,75 m de comprimento é mantido na posição vertical por um cabo e está preso a uma massa de 5,0 kg e um pivô na sua extremidade inferior

(Figura 10.45). O fio preso à massa de 5,0 kg passa sobre uma polia de massa e atrito desprezíveis e que puxa perpendicularmente ao poste. De repente, o cabo se rompe. a) Ache a aceleração angular do poste em torno do pivô assim que o cabo se rompe. b) A aceleração angular no item (a) permanece constante enquanto o poste cai (antes que atinja a polia)? Por quê? c) Qual é a aceleração da massa de 5,0 kg no instante em que o cabo se rompe? Essa aceleração permanece constante? Por quê?

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que um poste delgado e uniforme de 15,0   k g e 1,75   m de comprimento é mantido na posição vertical por um cabo e está preso a uma massa de 5,0   k g e um pivô na sua extremidade inferior.

O fio preso à massa de 5,0   k g passa sobre uma polia de massa e atrito desprezíveis e que puxa perpendicularmente ao poste. De repente, o cabo se rompe.

Com isso, queremos calcular a) a aceleração angular do poste em torno do pivô.

Queremos saber também b) se essa aceleração angular permanece constante.

Também queremos calcular c) a aceleração da massa de 5,0   k g no instante em que o cabo se rompe e se essa aceleração é constante.

Para isso, precisamos da segunda lei de Newton, ou seja:

F = m a

Onde F é a força, m é a massa e a é a aceleração.

E também da forma análoga da segunda lei de Newton para a rotação da polia, ou seja:

τ = I α

Onde τ é o torque, I é o momento de inércia e α é a aceleração angular.

Agora bora lá!! 😉

Passo 2

A aceleração a → da massa tem a mesma magnitude que a aceleração tangencial a t a n = r α do ponto no poste onde a corda está anexada.

Temos que r = 1,75 m - 0,500 m = 1,25 m

Vamos esboçar um diagrama de corpo livre para o poste e para a massa:

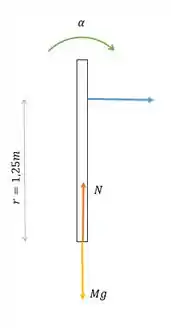
O poste tem sua inércia dada por:

I = 1 3 M L 2

Com: M = 15 k g L = 1,75 m .

Passo 3

  1. Nós vamos aplicar a forma análoga da segunda lei de Newton para a rotação de um corpo rígido para o poste:

    2. ∑ τ = I α

    ⇒ T   r = 1 3 M L 2 α

    Como a = r α , então α = a r , e:

    T = M L 2 3 r 2 a

    Passo 4

    E então, vamos aplicar a segunda lei de Newton a massa:

    ∑ F y = m a y

    ⇒ m g - T = m a

    Assim, estas duas ultimas equações nos dá que:

    m g = m + M L 2 3 r 2 a

    ⇒ a = m m + M L 2 3 r 2 g = 5 k g 5 k g + 15 k g ⋅ 1,75 m 2 2   3 ⋅ 1,25 m 2 g = 3,31 m / s 2

    E por fim, podemos calcular a aceleração angular:

    α = a r = 3,31 m / s 2 1,25 m = 2,65 r a d / s 2

    Passo 5

  2. Não. À medida que o poste gira e o ponto em que a corda está presa se move em um arco de um círculo, a corda não é mais perpendicular ao post.

    3. O torque devido a esta tensão muda e a aceleração devido a esse torque não é constante.

    Passo 6

  3. Do item (a), encontramos que a aceleração é igual a 3,31 m / s 2 . A aceleração da massa não é constante. Pois ela muda de acordo com a aceleração angular.

Resposta

  1. α = 2,65 r a d / s 2
  2. N ã o .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o sistema mostrado na Figura P10.21 com m 1=20,0k g , m 2=12,5k g , R=0,200m e a massa da roldana M=5,00k g . O corpo m 2 está repousando no chão, e o m 1 está 4,00m acima do chão quando é l
O braço na Figura P10.35 pesa 41,5N . A força gravitacional sobre ele age através do ponto A . Determine os módulos da força de tensão F → t no músculo deltoide e a força F → s exercida pelo ombro no
Uma viga uniforme repousando em dois pinos tem comprimento L=6,00m e massa M=90,0k g . O pino à esquerda exerce uma força normal n 1 sobre a viga, e o outro, localizado a uma distância l=4,00m da extr
Uma roda de oleiro – um disco grosso de pedra de raio 0,500m e m a s s a100k g – gira livremente a 50,0r e v / m i n . O oleiro pode parar a roda em 6,00s pressionando um pano úmido contra a borda e e
Uma força de F →= 2,00 i ^+3.00 j ^ N é aplicada a um corpo que é girado ao redor de um eixo fixo alinhado ao longo do eixo da coordenada z . A força é aplicada ao ponto r ^= 4,00 i ^+5.00 j ^ m . Enc