Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 43
Na preparação para um experimento que você fará em seu laboratório de introdução à física nuclear, você está olhando o lado interno de um tubo Geiger. Você mede o raio e o comprimento do fio central do tubo Geiger como e , respectivamente. A superfície externa do tubo é uma casca cilíndrica condutora que tem um raio interno de . A casca é coaxial com o fio e tem o mesmo comprimento (). Calcule
(a) a capacitância de seu tubo, considerando que o gás no tubo tenha uma constante dielétrica de , e;
(b) o valor da densidade linear de carga no fio quando a diferença de potencial entre o fio e a casca é de .
Passo 1
Cara, pela descrição, podemos supor que o tubo de Geiger é um tubo assim...
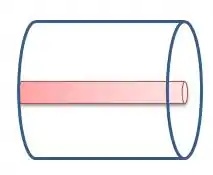
Ou ainda, vendo frontalmente...
Bem, como a capacitância é uma propriedade que depende apenas das propriedades geométricas, podemos medir a capacitância do cilindro usando a definição que vimos na teoria...
Então a letra A está no papo, neh?
Passo 2
Só que tem um detalhe! Ele nos disse que a constante dielétrica do gás que está no tubo . Isso significa que...
Então...
Conhecendo o comprimento do tubo () e os raios onde é o raio da casca esférica e , então...
Ou ainda...
Passo 3
Cara... Primeiro vamos calcular qual é a carga total quando a diferença de potencial entre a casca e o fio for de ...
Ou ainda, .
Passo 4
Então, com a carga calculada, podemos encontrar a densidade linear de carga no fio, sabendo que...
A área de um fio cilíndrico de raio , então...
Então, podemos dizer que a densidade linear de carga no fio será de...
Ou ainda...