Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 15
Na Figura 17.16, as faces grandes tanto das placas do capacitor quanto do bloco metálico que se insere entre as placas são quadradas, com lado . Certos vínculos permitem que o bloco metálico deslize livremente na horizontal, mantendo-se sempre equidistante das placas. Calcule a capacitância para (a) , (b) e (c) .
Passo 1
Vamos seguir a dica do problema e considerar que o sistema é uma combinação de dois capacitores e em paralelo:
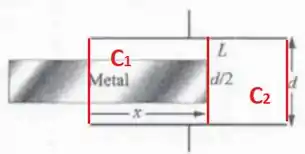
Para o capacitor temos que considerar que a distância entre as placas é , pois o campo elétrico dentro do metal é nulo e ele não contribuí para a ddp:
Já para :
Como os capacitores estão em paralelo, a capacitância equivalente será
Passo 2
Agora observe que as áreas e são dadas por
Assim,
Assim, para achamos
Já para temos
E para :
Resposta
Exercícios de Livros Relacionados
Se a distância entre as placas de um capacitor de placas paralelas, carregado e isolado é duplicada, qual é a razão entre as energias final e inicial armazenadas?
Se a carga em um condutor esférico isolado é duplicada, sua autocapacitância (a) dobra, (b) cai à metade, (c) permanece a mesma?
Verdadeiro ou falso: a densidade de energia eletrostática está uniformemente distribuída na região entre os condutores de um capacitor cilíndrico.
A tensão em um capacitor de placas paralelas cuja separação entre as placas é 0,500m m é 1,20k V . O capacitor é desconectado da fonte de tensão e a separação entre as placas é aumentada até que a ene
As placas de um capacitor de placas paralelas estão separadas por uma distância d e cada placa tem área A . O capacitor é carregado a uma diferença de potencial V e, então, é desconectado da fonte de