Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.4 - Ex. 12

A primeira figura mostra duas partículas carregadas mantidas fixas no eixo x a uma distância L uma da outra. A razão q 1 / q 2 entre os valores absolutos das cargas das duas partículas é 4,00 . A segunda figura mostra a componente x , E t o t , x do campo elétrico no eixo x , à direita da partícula 2, em função de x . A escala do eixo x é definida por x s = 30,0   c m , que é o último valor indicado no gráfico. (a) Para que valor de x > 0 o valor de E t o t , x , é máximo? (b) Se a carga da partícula 2 é - q 2 = -   3 e , qual é o valor do campo máximo?

Passo 1

Shooow galeraa, animados para continuar?

Então siiimbora!!

Bom, nós temos duas cargas de sinais opostos que irão causar um campo do lado direto da partícula 2, certo?

Nosso objetivo é obter o valor de x > 0 de modo que E t o t , x , é máximo e também se a carga da partícula 2 é - q 2 = -   3 e , qual é o valor do campo máximo.

Parece complicado? 🤔

Vamos colocar em um desenho:

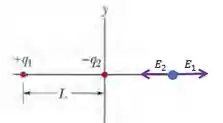
Vamos assumir que este campo está a uma distância x da origem, ok?

Teremos então um campo resultante sendo aplicado neste ponto, que podemos escrever assim:

E t o t a l = E 1 - E 2

Se lembram como calculamos o campo elétrico?

E = 1 4 π ε 0 . q r 2

Bora lá! 😬

Passo 2

Bom, olhando lá no gráfico que o problema nos deu nós conseguimos achar as distâncias da carga 1 e 2:

r 1 = L + x

r 2 = x

Substituindo na equação acima:

E t o t a l = 1 4 π ε 0 . q 1 L + x 2 - 1 4 π ε 0 . q 2 x 2

Colocando os termos em evidência, vamos ter que:

E t o t a l = 1 4 π ε 0 q 1 L + x 2 - q 2 x 2 = k q 1 L + x 2 - q 2 x 2

Lembrando que:

q 1 q 2 = 4 →       q 1 = 4 q 2

k = 8,99 × 10 9 N m 2 C 2

Então:

E t o t a l = 8,99 × 10 9 N m 2 C 2 4 q 2 L + x 2 - q 2 x 2

Nós precisamos achar o L , certo? E para isso vamos olhar no gráfico e ver que quando x = 20   c m o campo sera E t o t a l = 0 :

0 = q 2 8,99 × 10 9 N m 2 C 2 4 L + 20 2 - 1 20 2

4 L + 20 2 = 1 20 2

L + 20 2 20 2 = 4

Tirando a raiz:

L + 20 20 = 2

L + 20 = 40

L = 20   c m

Tranquilo até aqui? 😊

Passo 3

Boom, agora nós precisamos achar o valor de x cujo campo é máximo!

Do cálculo nós sabemos que para achar um ponto máximo derivamos a função e igualamos a zero.

Bora fazer isso??

d E t o t a l d x = q 2 k - 8 L + x 3 + 2 x 3 = 0

8 L + x 3 = 2 x 3

L + x 3 x 3 = 4

Tirando a raiz cúbica nos dois lados...

L x + 1 = 4 1 3

L x = 4 1 3 - 1

x = L 4 1 3 - 1 = 20   c m 4 1 3 - 1

x = 34   c m

Já achamos a letra (a) !!

Passo 4

Agora nós só precisamos achar a letra (b)!!

Ela nos diz que:

q 2 = 3 e = 4,8 × 10 - 19   C

E para que o campo seja máximo:

x = 34   c m

Substituindo tudo na equação do campo:

E t o t a l = 8,99 × 10 9 N m 2 C 2 4,8 × 10 - 19   C 4 0,34   m + 0,20 m 2 - 1 0,34   m 2

E t o t a l = 4,32 × 10 - 9 N m 2 C 4 0,2916   m 2 - 1 0,1156   m 2

E t o t a l = 2,2 × 10 - 8 N C

E chegamos ao fim!!

Entendeu tudo? Responde Aí! 😬

Resposta

a) x = 34   c m

b) E t o t , x = 2,2   x   10 - 8 N C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas minúsculas bolas de massa m possuem carga igual, porém contrárias de módulo q . Elas estão atadas ao mesmo gancho de teto por fios leves, de comprimento L . Quando um campo elétrico uniforme hori
Funcionamento de uma impressora a jato de tinta. Em uma impressora que usa jato de tinta, as letras são reproduzidas numa folha de papel injetando-se gotas de tinta, que saem de um pulverizador que se
Duas pequenas esferas de cobre possuem raio de 1m m cada uma. a)Quantos átomos cada esfera possui? b)Suponha que cada átomo de cobre contenha 29 prótons e 29 elétrons. Sabemos que elétrons e prótons p
Força elétrica dentro do núcleo. As dimensões típicas do núcleo atômico são da ordem de 10 - 15 m( 1f m ) . a)Se a distância entre dois prótons em um núcleo é de 2f m , ache o módulo da força elétrica
21.53 Uma carga elétrica positiva é distribuída sobre o eixo O y sendo λ a carga por unidade de comprimento. ( a ) Considere o caso para o qual a carga seja distribuída somente entre os pontos y=a ey=