Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.4 - Ex. 9
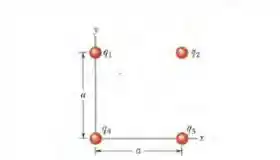
Na Fig. 22-32, as quatro partículas formam um quadrado de Iado e têm cargas , , e . Qual é o campo elétrico no centro do quadrado, em termos dos vetores unitários?
Passo 1
E aí! tudo certinho? 😁
O enunciado nos fala de quatro partículas que estão formando um quadrado e nós temos que calcular o vetor campo elétrico no centro do quadrado com os vetores unitários e .
Tem ideia de como fazemos isso? 😬
Para isso, iremos dividir o cálculo do campo elétrico em dois: e . Devemos lembrar da fórmula para calcular campo elétrico em um ponto que é:
Em que é a distância da carga até o ponto, é a carga e é a constante eletrostática (.
Mas como iremos calcular as componentes separadamente, iremos calcular o módulo do campo elétrico e decompor o vetor nos vetores unitários e .
Veja só! 😁
Passo 2
Mas como saberemos o sinal do vetor, já que iremos calcular o módulo? Lembre-se que partículas com carga positivo geram campo elétrico divergente (afastamento) e partículas com carga negativa geram campo elétrico convergente (atração). Assim, só precisamos desenhar as “setas” de acordo com isso. Bem, eu já desenhei e o desenho está abaixo:
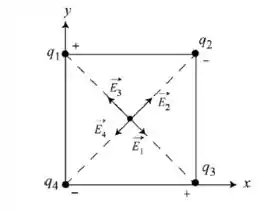
Pronto! Já desenhamos os vetores! Agora temos outra questão... Como vamos decompor esses vetores nos vetores unitários e ? Para isso, olhe a imagem abaixo:
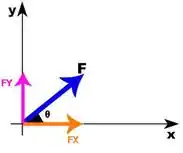
Você lembra da matéria de plano inclinado? Na figura acima, e . Com essa breve revisão podemos calcular e . Basta vê que as partículas formam um quadrado, então, o ângulo que cada vetor campo elétrico que a gente desenhou faz com os vetores unitários e é de 45°! Isso vai nos ajudar muito na hora de decompor os vetores.
Bora lá! 😉
Passo 3
Primeiramente, iremos calcular a componente do campo elétrico no centro do quadrado. Como , não precisamos nos preocupar nessa questão se vamos multiplicar por cosseno ou seno, porém vamos decompor corretamente porque vai que a questão da sua prova não seja 45° né?
Olhe a figura acima, no passo 1, viu que ? Então nós temos que calcular o módulo e multiplicar por .
Temos que tomar o cuidado porque e tem componentes de que são no sentido contrário ao crescimento do mesmo, portanto essas componentes serão com o sinal negativo. Lembre-se que a distância do centro até qualquer vértice do quadrado é
Chega de enrolação, vamos calcular!
Como e , temos
Tranquilo até aqui? 😉
Passo 4
Agora, nós temos que calcular a componente do campo elétrico. Para isso, nós iremos fazer do mesmo jeito. Note que e tem sinal negativo da componente y e agora devemos multiplicar por devido a primeira figura, lembra? Vamos aos cálculos!
Substituindo os valores dados...
Agora nós podemos desenhar o vetor campo elétrico total, :
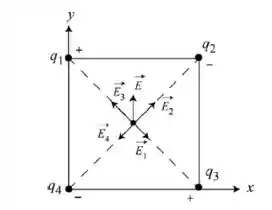
E aí! entendeu tudo? Responde Aí! 😊