Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 73
Nos Problemas de a , lhe são fornecidas uma ou mais equações cinemáticas para usar na resolução de um problema. Para cada um deles, você deve:
. Redigir um problema realista para o qual esta ou estas equações se apliquem. Tenha certeza de que sua resposta seja consistente com as equações fornecidas.
. Esboçar uma representação pictórica de seu problema.
. Encontrar a solução para o problema proposto.
73.
Passo 1
Então galera, primeiro vamos tentar identificar que equação é essa e depois ver o que é fornecido por ela sabendo dessas coisas podemos pensar em um problema para essa situação como pede em .
Eu vou apresentar um problema para isso, mas você é livre para criar outro desde que ele seja realista.
Sabendo o que a equação nos fornece e que equação ela é podemos montar um esquema pictórico da situação, mesmo que criemos problemas diferentes esse esquema vai ser igual para ambos os casos já que vamos montar ele a parti das informações da equação.
E para o item basta encontrarmos a solução do nosso problema que independentemente de como foi escrito será o valor de que é a velocidade final na direção .
Passo 2
Vamos lá então, temos a seguinte equação:
Comparando-a com as equações de cinemática que conhecemos temos que ela é a equação de Torricelli, que para a direção tem a seguinte forma:
Comparando com a equação do enunciado temos que:
Olhando essas informações podemos deduzir que o movimento começa de baixo para cima e em o objeto tem uma velocidade de e ele sofre uma aceleração para baixo devido a sinal de negativo.
Passo 3
Com as informações do passo anterior podemos formular o seguinte enunciado para essa situação.
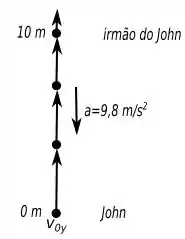
Em um belo dia, John está deitado no gramado e jogando uma bola de tênis para cima. Até que seu irmão que estava na janela do segundo andar da casa a uma altura de percebeu que a bolinha passou por ele a uma velocidade de . Então o irmão de John o desafia a descobrir qual a velocidade com que John lançou a bolinha. Você pode ajudar John nisso?
Passo 4
Agora a representação pictórica dessa situação é a seguinte:
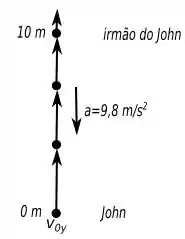
Passo 5
Agora vamos fazer o que o item quer, temos que resolver o problema que criamos, que vai ser encontrar o valor de , temos o seguinte:
Isolando , temos que:
Então temos que:
Resposta
Em um belo dia, John está deitado no gramado e jogando uma bola de tênis para cima. Até que seu irmão que estava na janela do segundo andar da casa a uma altura de percebeu que a bolinha passou por ele a uma velocidade de . Então o irmão de John o desafia a descobrir qual a velocidade com que John lançou a bolinha. Você pode ajudar John nisso?
