Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 81

81. Um velocista pode acelerar com aceleração constante durante 4,0   s antes de atingir sua velocidade máxima. Ele consegue correr os 100   m rasos em 10   s . Qual é o valor de sua velocidade ao cruzar a linha de chegada?

Passo 1

O enunciado nos diz que o velocista possui uma aceleração constante. Segundo a tabela 2.2 temos três equações cinemáticas do movimento com aceleração constante.

Para saber qual vamos usá-las temos que analisar o que o enunciado pede e o que ele nos dar, mas fica de boa que no próximo Passo 3 vamos analisar isso devagar.

Vamos usar também modelo de partículas para uma melhor visualização do problema.

Passo 2

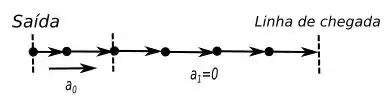
Durante 4,0   s o velocista se move com aceleração constante, ou seja, a velocidade aumenta de forma proporcional até t = 4,0   s

Ao chegar na velocidade máxima ele não consegue mais acelerar então sua aceleração será a 1 = 0 até atingir t = 10   s .

Ou seja:

Passo 3

Vamos juntar agora todas as informações:

O corredor vai de x 0 até x 1 com aceleração constante chegando em x 1 em t = 4   s

x 0 = 0 , v 0 = 0 , t 0 = 0

x 1 =   ? , v 1 = ?   , t 1 = 4   s

Depois de x 1 até x 2 , sem acelerar, chegando em x 2 em t = 10   s .

x 1 =   ? , v 1 = ?   , t 1 = 4   s

x 2 =   100   m , v 2 =   ?   , t 2 = 10   s , a 1 = 0

Como o percurso de x 1 para x 2 o corredor faz sem acelerar, podemos afirmar que v 1 = v 2 .

Então vamos achar v 1 para resolver a questão.

Passo 4

Achando v 1 :

Através da equação 2.20 temos que:

x 2 = x 1 + v 1 t 2 - t 1 + 1 2 a 1 ( t 2 - t 1 ) ²

Substituindo os valores:

100   m = x 1 +   v 1 10   s - 4   s - 1 2 ⋅ 0 10   s - 4   s 2

⇒ 100   m = x 1 +   v 1 10   s - 4   s

Porém não sabemos quem é x 1 , então vamos descobrir usando a mesma equação na primeira parte do percurso.

Passo 5

Achando x 1 :

x 1 = x 0 + v 0 t 1 - t 0 + 1 2 a 0 ( t 1 - t 0 ) ²

Substituindo os valores:

x 1 = 0   m + 0 ⋅ 4   s - 0   s + 1 2 a 0 4   s - 0   s 2 = 8   s 2   a 0  

Mas não conhecemos a 0 então teremos de usar mais uma equação da cinemática para encontrar.

Passo 6

Achando a 0 :

A equação que iremos usar será a equação 2.18 , ou seja:

v 1 = v 0 + a 0 t 1 - t 0 → a 0 = v 1 4   s

Substituindo no valor de x 1 no Passo 5:

x 1 = 8   s 2   a 0 = 8   s 2 ⋅ v 1 4   s = 2   s v 1  

Prontinho, estamos quase acabando. Agora só falta substituir esse valor de x 1 na última equação do Passo 4 pois aí vamos conseguir o valor final que queremos.

Passo 7

Achando v 1 :

100   m = x 1 +   v 1 6 s

Substituindo o valor de x 1 :

100   m = 2   s v 1 +   v 1 6 s = 8   s v 1 → v 1 = 100   m 8   s = 12,5   m / s

Ou seja:

v 2 = v 1 = 12,5   m / s

Resposta

v 2 = 12,5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um piloto voa horizontalmente a 1300k m / h a uma altura h = 35 m acima do solo inicialmente plano. No instante t = 0 , o piloto começa a sobrevoar um terreno inclinado para cima de um ângulo θ = 4,3
No instante em que um sinal de trânsito fica verde, um automóvel começa a se mover com uma aceleração constante a de 2,2m / s 2 . No mesmo instante, um caminhão, que se move com uma velocidade constan
Um carro de corrida é capaz de acelerar de 0 a 60k m / h em 5,4s . (a) Qual é a aceleração média, em m / s ² ², durante este intervalo? (b) Qual é a distância percorrida pelo carro em 5,4s , supondo q
O tempo necessário para frear um carro pode ser dividido em duas partes: o tempo de reação para o motorista começar a frear e o tempo necessário para que a velocidade chegue a zero depois que o freio
A Fig. 2-42 mostra um dispositivo simples que pode ser usado para medir o seu tempo de reação: uma tira de papelão marcada com uma escala e dois pontos. Um amigo segura a tira na vertical, com o poleg