Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 55
Um próton (massa de 1 u) é lançado contra um núcleo-alvo com velocidade de . O próton ricocheteia com sua velocidade reduzida em , enquanto o núcleo-alvo adquire uma velocidade de . Qual é a massa, em unidades de massa atômica, do núcleo-alvo?
Passo 1
Agora desconhecemos a massa grandona da questão anterior, porém sabemos que o comportamento de ambos antes e depois do choque é igual a:
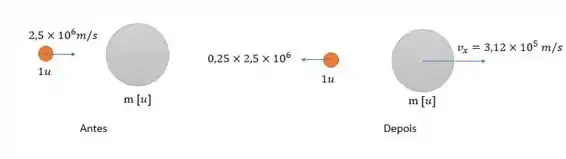
Uma vez que o próton ricocheteia (bate e volta) e terá um módulo de velocidade igual a:
Estatística básica, se reduzimos a velocidade em então a velocidade está a da velocidade original (pegadinha de enunciado).
E como a velocidade tem sentido para a esquerda então:
Passo 2
Pela conservação do momento linear temos que:
Resposta
Exercícios de Livros Relacionados
(b) Descreva o movimento das duas extremidades do bastão no referencial do centro de massa do bastão.
26. Um bastão, com a extremidade mais massiva que a outra é lançado, é lançado no ar, a um ângulo não nulo com a vertical.(a) Descreva a trajetória do centro de massa do bastão no referencial do chão.
20. Uma zarabatana dupla é mostrada na figura 8-41. O ar é soprado no lado esquerdo, e duas ervilhas idênticas A e B estão colocadas dentro de cada canudo, como mostrado. Se a zarabatana é mantida na
30. Um carro de 2000 K g viajando a 90 K m / h bate contra uma parede imóvel de concreto.(a) Estime o tempo da colisão, supondo que o centro do carro percorre metade de sua distância até a parede, com
31. Em corridas de vagonetes ferroviários movidos a alavanca manual, uma rapidez de 32,0K m / h foi atingida por equipes de quatro pessoas. Um vagonete de 350K g de massas se move com esta rapidez, at