Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 125
Prove que, se um espelho plano for girado de um ângulo , o raio refletido girará de um ângulo .
Passo 1
Fala galerinha, beleza?
Esse é um exercício bem bobinho de geometria, mas temos que fazer com bastante calma para não fazer nenhuma besteira. Primeiro vou desenhar os espelhos e as respectivas normais. Em preto o primeiro espelho e, em vermelho, o espelho rotacionado por :
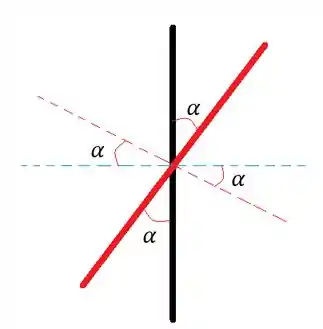
Repare que as normais também giram por um ângulo .
Passo 2
Na próxima figura eu desenhei o raio incidente em verde e os raios refletidos por cada espelho. Do espelho o raio está em verde, do espelho vermelho o raio está em laranja:
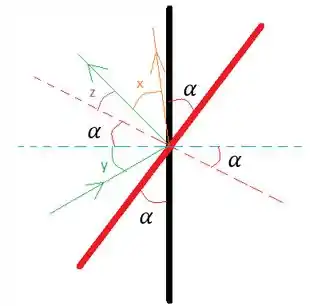
Observe que é o ângulo de incidência no espelho preto e é o ângulo de reflexão correspondente, de modo que
Da mesma forma, o raio incidente no espelho vermelho é , enquanto o raio refletido é :
Nosso objetivo é achar :
Fazendo a primeira equação menos a segunda:
Assim,
Era exatamente isso que o exercício pediu para gente mostrar!
Resposta
Demonstração.