Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas Adicionais - Ex. 89

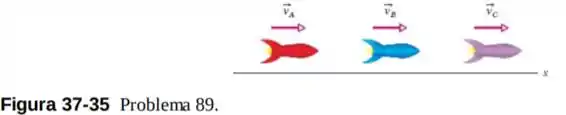
Na Fig. 37-35, três espaçonaves estão viajando na mesma direção e no mesmo sentido. As velocidades das espaçonaves em relação ao eixo x de um referencial inercial (a Terra, por exemplo) são v A = 0,900 c , v B e v C = 0,800 c . (a) Qual deve ser o valor de v B para que as naves A e C se aproximem da nave B com a mesma velocidade relativa? (b) Qual é essa velocidade relativa?

Passo 1

Fala galerinha, beleza? Bora resolver um probleminha sobre relatividade?

A sacada para resolver o problema é passar as velocidades para o referencial de v B . Vamos chamar esse referencial de S ' , enquanto o referencial do desenho é S .

Em S , temos que

v A = + 0,900   c                       v C = + 0,800   c

A velocidade de S ' com relação a S é v B .

A fórmula que transforma as velocidades do referencial S para o referencial S ' é

u ' = u - v 1 - u v c 2

Nessa última expressão, u é a velocidade medida em S , u ' é a velocidade medida em S ' e v é a velocidade de S ' com relação a S . Com isso, as velocidades das naves A e C, vistas por um observador na nave B (em S ' ), são

v A ' = v A - v B 1 - v A v B c 2                 e             v C ' = v C - v B 1 - v C v B c 2

Substituindo v A e v C :

v A ' = 0,9 c - v B 1 - 0,9 c ⋅ v B c 2                   e           v C ' = 0 , 8 c - v B 1 - 0 , 8 c ⋅ v B c 2

Passo 2

Para que as velocidades relativas de aproximação à nave B sejam iguais, devemos ter

v A ' = - v C '

O sinal de menos aparece pois para ambas as naves estarem se aproximando da nave B, elas devem estar se movendo em sentidos contrários.

Assim,

0,9 c - v B 1 - 0 , 9 v B c = - 0,8 c - v B 1 - 0,8 v B c

Para melhorar a relação, vamos escrever:

c 0,9 - β 1 - 0,9   β = c β - 0,8 1 - 0,8 β ,                 β = v B c

Simplificando c e multiplicando em cruz:

0,9 - β 1 - 0,8 β = 1 - 0,9 β β - 0,8

0,9 - 0,72 β + 0,8 β 2 - β = β - 0,8 - 0,9 β 2 + 0,72 β

1,7 β 2 - 3,44 β + 1,7 = 0

As soluções dessa equação do segundo grau são

β = 0,858               o u             β = 1,166

Como β ≤ 1 , temos que

v B c = 0,858

Assim, a velocidade da nave B deve ser

v B = 0,858   c

Passo 3

A velocidade relativa será simplesmente:

v A ' = 0,9 c - v B 1 - 0,9 c ⋅ v B c 2 = 0,9 c - 0,858   c 1 - 0,9 c ⋅ 0,858   c c 2

Fazendo as contas:

v A ' = - v C ' = 0,185   c

Resposta

v A ' = - v C ' = 0,185   c

v B = 0,858   c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A transformação de Lorentz para y e z é igual ao resultado clássico: y = y ′ e z = z ′. No entanto, a transformação relativística da velocidade não dá o resultado clássico uy = u 'y e z z u = u'. Expl
Uma nave espacial, em repouso em um determinado referencial S, recebe um aumento de velocidade de 0,50c (chame esse aumento de boost 1). Em relação ao seu novo quadro de repouso, a nave recebe um aume
Uma nave espacial está se movendo para o leste a uma velocidade de 0,90c em relação à Terra. Uma segunda espaçonave está se movendo para oeste à velocidade de 0,90c em relação à Terra. Qual é a veloci
Para luz que é deslocada por Doppler em relação a um observador, definimos o parâmetro de desvio para o vermelho z = () f - f ′ f ′, onde f é a frequência da luz medida no quadro de repouso do emissor
Um feixe de luz se move ao longo do eixo y ′ com velocidade c no quadro S ′, que está se movendo na direção + x com velocidade v em relação ao quadro S. (a) Encontre os componentes xey da velocidade d