Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 51
Pulando para o solo. Um homem de pula de uma plataforma de de altura acima do solo. Ele mantém as pernas esticadas à medida que cai, mas no momento em que os pés tocam o solo, os joelhos começam a se dobrar, e, considerando-o uma partícula, ele se move antes de parar.
- Qual é sua velocidade no momento em que os pés tocam o solo?
- Qual é sua aceleração (módulo e direção) quando ele diminui de velocidade, supondo uma aceleração constante?
- Desenhe o diagrama do corpo livre para ele. Em termos das forças que atuam no diagrama, qual é a força resultante sobre ele? Use as leis de Newton e os resultados do item para calcular a força média que os pés dele exercem sobre o solo enquanto ele diminui a velocidade. Expresse essa força em newtons e também como um múltiplo do peso dele.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um homem de pula de uma plataforma de de altura acima do solo.
Ele mantém as pernas esticadas à medida que cai, mas no momento em que os pés tocam o solo, os joelhos começam a se dobrar, e, considerando-o uma partícula, ele se move antes de parar.
Queremos calcular a velocidade no momento em que seus pés tocam no solo e sua aceleração (módulo e direção) quando ele diminui de velocidade, supondo uma aceleração constante.
Para isso, precisaremos aplicar alguns princípios de movimento retilíneo uniformemente variado (MRUV).
Por fim, temos que desenhar o diagrama de corpo livre do homem, ou seja, temos que verificar todas as forças e suas direções que estão atuando no homem.
E aí?? Bora lá?!! 😉
Passo 2
Enquanto ele está caindo, ele está desenvolvendo um movimento de queda livre (MQL) com aceleração constante de direcionada para baixo.
Até um segundinho antes dos pés dele tocarem ao chão ele está em queda livre, então podemos usar as equações de movimento para determinar a velocidade final dele.
Os dados que o problema dá são:
Beleza? Daí vamos lembrar da equação que envolve essas quantidades:
Onde é a velocidade final, é a velocidade inicial, é a aceleração e é a variação da altura.
No caso de queda livre a aceleração é negativa e a fórmula fica assim:
Onde é a aceleração da gravidade.
Lembrando que , agora é só substituir e determinar a velocidade do homem:
Passo 3
Agora o problema pede a aceleração enquanto ele dobra os joelhos até parar.
A velocidade inicial (nessa parte do movimento) é e a final é zero.
Ele percorre uma distância de e quer saber qual é a aceleração .
Bom, vou usar a mesma relação que usei no passo anterior:
Mas agora não vou impor nenhum sinal para ! Basta substituir os valores:
Aqui encontramos uma aceleração negativa! Sim, ela é a aceleração necessária para parar o corpo, então está correto! E ela é vertical para cima!
Passo 4
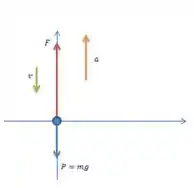
No homem estão agindo duas forças: a força peso verticalmente para baixo e a força que o solo faz sobre ele, verticalmente para cima.
A força peso está representada em azul. Já a força vertical está em vermelho.
A velocidade (representada em verde) do homem é negativa (descendo) e ela está diminuindo em módulo, então a aceleração (representada em laranja) deve ser positiva, ou seja, vertical para cima.
A força resultante acompanha o sentido da aceleração, consequentemente ela é vertical para cima.
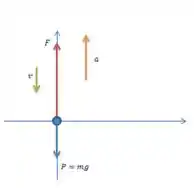
Juntando todas essas informações podemos fazer o diagrama:
Passo 5
Usando a segunda lei de Newton no homem temos:
A força é o que queremos saber, o peso é dado por , a aceleração já foi determinada no passo anterior e vale , agora é só substituir:
Assim a força em newtons é , ou em relação ao peso dele:
Assim a força que o chão faz sobre ele (que é a mesma que ele faz sobre o chão) é aproximadamente vezes o seu peso!
Resposta
