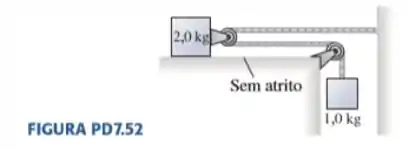
Quanto vale a aceleração do bloco de 2,0 kg sobre a mesa livre de atrito da FIGURA PD7.52?

Sugestão: reflita cuidadosamente sobre o vínculo de aceleração.

Primeiro vamos no esquema

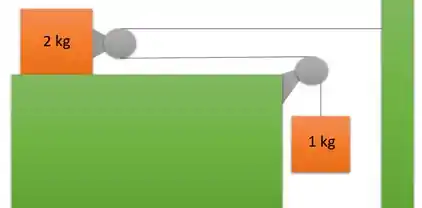
Vemos que tem duas polias e dois bloco de massa 2 kg e de 1 kg. Vamos analisar como dois sistemas? Então o primeiro sistema será

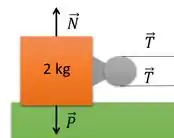
Percebemos que na vertical tem duas forças, o Peso e a Normal , mas ela é nula, pois não interfere no movimento. Já na horizontal temos das Trações que irá conduzir o movimento do bloco A. Assim podemos dizer

E o segundo sistema com o bloco B

Ele não possui forças horizontais, significando que ele vai movimento da vertical, assim

Sabemos que o é , assim é , e o Peso é . Substituindo

Belezinha, chegamos até aqui, mas podemos simplificar mais ainda! O bloco A andar certa quantidade (s), mas a quantidade que desce do bloco B é o dobro! Isso implica que a aceleração 1 é o dobro da aceleração 2

Agora indo para a parte algébrica

Substituindo

Só que ele pede do primeiro bloco, substituindo